"2조(스피노)"의 두 판 사이의 차이
Uosche2512 (토론 | 기여) (→완료작품의 평가) |
Uosche2512 (토론 | 기여) (→특허 출원 내용) |
||
| 313번째 줄: | 313번째 줄: | ||
3) 딥러닝 검증 기술 및 해석 가능성 기여 | 3) 딥러닝 검증 기술 및 해석 가능성 기여 | ||
신뢰성과 안전성이 요구되는 분야에서 딥러닝 모델의 검증 가능성 확보는 필수적이다. 본 연구는 ReLU 기반 신경망의 MILP 표현을 계산적으로 실현 가능한 수준으로 단순화함으로써, 자율주행, 의료 AI, 항공우주 시스템 등의 안전성 검증에도 기여할 수 있다. 이는 신경망 검증을 위한 MILP 접근법의 산업 적용 가능성을 크게 넓히는 효과를 가진다. | 신뢰성과 안전성이 요구되는 분야에서 딥러닝 모델의 검증 가능성 확보는 필수적이다. 본 연구는 ReLU 기반 신경망의 MILP 표현을 계산적으로 실현 가능한 수준으로 단순화함으로써, 자율주행, 의료 AI, 항공우주 시스템 등의 안전성 검증에도 기여할 수 있다. 이는 신경망 검증을 위한 MILP 접근법의 산업 적용 가능성을 크게 넓히는 효과를 가진다. | ||
| − | |||
| − | |||
| − | |||
2025년 6월 7일 (토) 23:42 판
프로젝트 개요
기술개발 과제
국문 : ReLU 신경망 기반 MILP 최적화에서 OBBT 기법을 통한 계산 효율 개선 연구
영문 : Improving Computational Efficiency in MILP Optimization of ReLU Neural Networks via OBBT
과제 팀명
스피노
지도교수
유준재 교수님
개발기간
2025년 3월 ~ 2025년 6월 (총 4개월)
구성원 소개
서울시립대학교 화학공학과 2019340042 이학균(팀장)
서울시립대학교 화학공학과 2019340041 이창형
서울시립대학교 화학공학과 2021340013 박근영
서울시립대학교 화학공학과 2021340047 진주희
서론
개발 과제의 개요
개발 과제 요약
◇ 본 개발과제는 ReLU 활성화 함수를 가진 인공신경망(ANN)이 내장된 혼합정수최적화(MILP) 문제의 효율적인 해결 방안을 모색하는 데 목적이 있다. ReLU 기반 신경망이 포함된 최적화 문제는 big-M 계수의 증가로 인해 계산 복잡도가 급격히 증가하는 한계를 지닌다.
◇ 본 연구에서는 이러한 한계를 극복하기 위해 신경망 훈련 단계에서 적용할 수 있는 L1 Regularization, Dropout 기법을 도입하였으며, 훈련 이후에는 최적화 기반 Bound Tightening(OBBT) 및 Big-M 계수를 감소시키기 위한 새로운 기법을 제안하였다.
◇ 특히, 메탄(CH₄)과 CLS 공정 기반의 실제 수소 생산 시뮬레이션 데이터를 활용하여, 다중 입력 조건에 대한 수소 생산량을 최대화하는 MILP 문제를 정의하고 최적화함으로써, 제안 기법의 실질적인 활용 가능성과 계산 효율성을 입증하고자 하였다.
◇ 수치 실험을 통해 각 기법의 효과를 선형 영역의 수, 안정적 뉴런의 비율, 계산 효율성 측면에서 비교 분석하였으며, 최종적으로 실제 공정 문제 해결에서의 MILP 적용 가능성과 계산 효율 향상 효과를 검증하는 것을 목표로 한다.
개발 과제의 배경
◇ 최근 다양한 산업 및 공학 분야에서 인공지능과 머신러닝 기반의 최적화 기술이 중요한 역할을 수행하고 있다. 특히 제조 공정 최적화, 공급망 관리, 에너지 시스템 운영 등 복잡한 비선형 관계를 다루는 문제들에서 높은 정확도와 표현력을 지닌 ReLU 기반 인공신경망이 적극적으로 도입되고 있다.
◇ 그러나 ReLU 활성화 함수를 이용한 신경망의 경우, 모델의 깊이가 증가함에 따라 Big-M 계수가 지수적으로 커지는 현상으로 인해 최적화의 계산적 비효율성이 증가하는 한계가 존재한다.
◇ 본 연구에서 제안된 L1 정규화, Bound Tightening 등의 기법은 이러한 Big-M 계수 문제를 해결하여 신경망 내장 최적화 모델의 계산 효율성을 획기적으로 개선할 수 있다. 이는 최적화 모델의 정확성과 효율성을 동시에 향상시키고, 복잡한 산업 환경에서의 추론 속도와 신뢰성을 높이는 데 크게 기여할 것으로 예상된다. ◇ 특히, 본 연구는 수소 생산 공정 최적화라는 실제 산업적 문제에 적용됨으로써, 그 실효성을 입증하였다. CH₄와 CLS 기반의 수소 제조 공정은 탄소중립 시대에 친환경 연료 생산 수단으로 각광받고 있으며, 수소 생산 효율을 극대화하는 공정 조건의 탐색은 에너지 효율성과 경제성 모두를 좌우하는 핵심 과제이다. 따라서 본 연구는 단순한 이론적 개선을 넘어, 탄소 배출 저감 및 청정에너지 전환이라는 사회적 요구에 기술적으로 기여할 수 있는 기반을 마련했다.
◇ 결과적으로, 본 연구의 성과는 다양한 산업 및 공학적 문제 해결의 실질적 효용성을 높이고, 특히 청정 연료 생산, 에너지 공정 최적화, 스마트 제조 등 분야에서 운영 비용 절감과 환경적 지속가능성 향상에 전문적인 도움을 줄 수 있을 것으로 기대된다.
개발 과제의 목표 및 내용
◇ 본 개발 과제의 주요 목표는 ReLU 기반 인공신경망 모델이 포함된 혼합정수최적화(MILP) 문제의 효율성을 높이는 신경망 훈련 및 최적화 기법을 개발하고, 이를 실제 산업 공정에 적용 가능한 수준으로 발전시키는 것이다. 이를 위해 다음과 같은 구체적인 내용을 수행하였다.
1. ReLU 활성화 함수 기반 신경망의 구조적 한계 분석 및 문제점 도출 2. L1 Regularization과 Dropout을 활용한 모델 중복성 감소 및 효율성 향상 방안 연구 3. 최적화 기반 Bound Tightening(OBBT)을 통한 Big-M 계수의 효율적 감소 방안 개발 4. 신경망 스케일링 기법 개발을 통한 Big-M 계수 추가 감소 및 계산 효율성 향상 5. 수치적 실험을 통한 제안된 기법들의 성능 검증 및 실제 적용 가능성 평가
◇ 특히, CH₄ + CLS 비재순환 수소 생산 공정 모델에서 다수의 입력 변수(물질 유량, 반응 온도 등)를 조절하여 수소 생산량을 최대화하는 MILP 최적화 문제를 구성하고, 본 연구에서 제안한 신경망 기반 기법들을 적용함으로써 이론적 기법의 실제 공정 최적화로의 확장 가능성을 확인하였다.
◇ 본 연구의 결과는 신경망 기반 최적화 기술의 계산적 한계를 효과적으로 극복함과 동시에, 복잡한 연속 공정에서도 데이터 기반의 정밀한 조건 탐색과 계산 효율성 개선이 가능함을 입증하며, 이를 통해 산업 현장의 최적 운전 조건 도출, 생산성 향상, 에너지 절감 등 실질적이고 전문적인 기여가 가능할 것으로 기대된다.
관련 기술의 현황
관련 기술의 현황 및 분석(State of art)
- 전 세계적인 기술현황
ReLU 기반 신경망을 MILP(Mixed-Integer Linear Programming) 형식으로 변환하여 수학적으로 해석 가능한 방식으로 활용하려는 연구가 활발하게 이루어지고 있다. 특히, 최적화 문제나 신뢰성 검증(adversarial verification), 공정 제어 및 설계 최적화 등 실제 산업계에 적용 가능한 신경망 모델을 만들기 위해 MILP 기반 포뮬레이션이 주목받고 있다. 이에 따라, MILP 포뮬레이션을 구성할 때 발생하는 주요 난제 중 하나인 big-M 계수의 과대 추정 문제를 해결하기 위한 다양한 bound tightening 기법이 연구되고 있다. 최근에는 Optimization-Based Bound Tightening (OBBT), ReLU stability regularization, ReLU scaling, convex hull 표현 방식 등 다양한 수학적 기법들이 제안되었으며, 이를 통해 solver 계산 시간 단축, stable neuron 비율 증가, MILP feasibility 향상 등의 성능 개선이 보고되고 있다. 그러나 여전히 대부분의 연구는 MILP 구조의 이론적 정교화에 집중되어 있으며, bound 조절 기법의 정량적 효과를 다양한 조건에서 비교한 실험 기반 연구는 드물다.
- 특허조사 및 특허 전략 분석
◇ Grimstad & Andersson (2019)은 ReLU 신경망을 surrogate model로 사용하여 MILP 문제 내에 삽입하고, solver 기반 최적화를 수행하는 전략을 제시하였다. 신경망 기반의 예측 모델을 제약조건이나 목적함수에 통합함으로써 MILP 문제의 확장 가능성을 입증하였으나, bound 조건은 고정된 단순 추정값에 의존하였다.
◇ Tsay et al. (2021)은 big-M 방식의 한계를 극복하기 위해 입력 공간을 구간으로 분할하고, 각 구간에 대해 ReLU 조건을 수학적으로 모델링하는 partition-based formulation을 제안하였다. 이 기법은 MILP의 구조적 표현력을 개선하는 데 효과적이지만, 여전히 bound는 입력 구간에 고정되며, solver 성능을 실험적으로 분석하는 데 초점은 약했다.
◇ Xiao et al. (2019)은 adversarial robustness verification 문제에서 ReLU 안정성(ReLU stability)을 학습 중에 유도함으로써, MILP 내 뉴런 분기를 줄이고 계산 효율성을 향상시키는 방식을 제안하였다. 이는 학습 기반 사전 구조 최적화 전략으로, bound 설정을 개선하는 방식은 아니었다.
이처럼 기존 연구들은 모두 ReLU 신경망의 MILP 변환 구조 또는 안정성 확보를 위한 학습 전략에 집중하고 있으며, 입력 조건에 따라 bound를 동적으로 조정하여 solver 성능을 실험적으로 극대화한 연구는 제한적이다. 이는 본 과제가 기존 연구 및 특허와 명확히 차별화되는 핵심 지점이다.
◇ Grimstad & Andersson (2019) 이 연구는 ReLU 신경망을 surrogate model로 활용하여 MILP 내 목적함수 또는 제약식에 통합하는 전략을 제시한다. 이 접근은 모델 기반 최적화(model-based optimization) 측면에서 가치가 높으며, 신경망 예측 모델의 MILP 통합 기법에 대한 특허 전략으로 이어질 수 있다. 특히 구조 자체는 기존 MILP의 틀을 크게 벗어나지 않으면서, surrogate model을 데이터 기반으로 확장해 적용할 수 있는 유연성을 제공한다. 따라서 해당 연구는 신경망 기반 최적화 프레임워크 설계 및 응용 구조에 대한 기술 보호가 핵심 전략이 된다.
◇ Tsay et al. (2021) 이 논문은 Big-M 계수 없이도 ReLU를 MILP로 정밀하게 표현할 수 있는 partition-based formulation을 제시한다. 입력 공간을 분할한 뒤, 각 구간에 대해 분리된 제약조건을 도입함으로써 수학적으로 더 강건한 구조를 형성하며, 이 구조 자체가 특허의 주 대상이 될 수 있다. 이 전략은 알고리즘 또는 solver 내장 최적화 방식으로 구현될 수 있어, MILP 포뮬레이션 기법의 구조적 설계 특허로 전환 가능하다. 또한 solver 성능에 직접 연결되므로, 산업용 solver 제품군에 통합될 수 있는 형태의 원천 기술 보호 전략으로 적합하다.
◇ Xiao et al. (2019) 이 연구는 신경망 학습 단계에서 ReLU 뉴런의 stability를 유도하는 훈련 전략을 통해 MILP 검증 과정의 계산 효율을 높이는 방식이다. 이는 MILP 구조 자체보다는, 학습 알고리즘을 조정하여 MILP 계산 부담을 사전적으로 줄이는 간접 최적화 전략에 해당한다. 이 전략은 신경망 학습 방법론에 가까워, regularization 또는 loss function 설계에 관한 특허로 이어질 수 있으며, MILP 기반 검증 외에도 다양한 구조화 학습 문제에 일반화되어 적용될 수 있다. 따라서 해당 연구는 학습-검증 통합 프레임워크에 대한 알고리즘 특허 전략으로 접근 가능하다.
이들 전략의 공통점은 미리 정의된 bound 또는 근사값에 기반해 MILP 구조를 구성한다는 점이다. 그러나 이는 실제 문제 상황에서 발생하는 비효율적인 big-M 추정을 야기할 수 있으며, 계산 자원의 낭비로 이어진다. 이에 비해 우리 프로젝트는 ReLU 뉴런의 pre-activation bound를 각 조건에 맞추어 LP 기반으로 최적화(OBBT) 함으로써, MILP 구조는 그대로 유지하면서도 solver 성능을 직접 개선하는 전략을 택하고 있다. 이는 실용성과 일반화 가능성 측면에서 유리하며, 향후 OMLT, Pyomo, Gurobi 등의 연계 환경에서도 쉽게 확장 가능한 특허 전략으로 이어질 수 있다.
개발과제의 기대효과
기술적 기대효과
1. ReLU 기반 신경망의 MILP 최적화 성능 향상 · 본 연구에서 제안한 L1 정규화, Dropout, OBBT, scaling 기법을 통해 기존 방식 대비 solver 계산 시간과 메모리 사용량을 현저히 감소시킬 수 있음. · 특히, OBBT와 scaling 기법을 적용함으로써 Big-M 계수를 크게 줄이고, stable neuron 비율을 증가시켜 MILP 구조의 연산 효율을 극대화함. · 이는 실제 CH₄ + CLS 기반 수소 생산 공정 최적화 문제에 적용되었으며, 다변수 입력 조건 하에서 수소 생산량을 최대화하는 최적 운전 조건을 효율적으로 도출함으로써 이론 기법의 산업 공정 적용 가능성을 입증함.
2. 복잡계 최적화 문제에 대한 신경망 내장 구조 자동화 기반 마련 · Pyomo, OMLT, Gurobi 등 최적화 도구와 연계 가능한 범용 신경망 기반 MILP 구조를 실험을 통해 검증하였으며, 이는 실제 공정 모델에서 수치 시뮬레이션 데이터를 surrogate 모델로 학습하고 MILP 형식으로 변환해 최적화까지 연결하는 자동화 체계로 구현됨. · 향후 chemical process optimization, 생산계획, logistics 최적화 등 다양한 복잡계 문제군에 바로 적용 가능한 통합형 프레임워크로 확장 가능함.
3. 설계·제어·검증 통합형 AI 최적화 모델 기반 구축 · 학습된 신경망을 단순한 예측 도구로 활용하는 것을 넘어, 수학적 최적화 문제 내에 직접 내장하여 설계–제어–검증까지 통합하는 End-to-End 수리 최적화 모델 구현이 가능함. · 이는 공정 운영 자동화, 조건 설정 최적화, 시나리오 기반 제어 등 고신뢰 AI 기반 시스템 구축에 활용될 수 있으며, explainable AI 및 산업 AI 최적화 모델 개발 측면에서도 중요한 기술적 진보로 평가됨.
경제적, 사회적 기대 및 파급효과
1. 산업계의 최적화 수요에 대한 고성능 솔루션 제공 · 에너지, 화학공정, 반도체 제조, 바이오 생산 등 계산 성능이 병목이 되는 분야에서, MILP 기반 신경망 최적화 모델을 통해 고속·고정밀 의사결정이 가능해짐. · 특히 시뮬레이션 비용이 높은 공정 설계나 생산 공정 제어 분야에서 실질적인 비용 절감 효과가 기대됨.
2. 데이터 기반 의사결정의 신뢰성 제고 · 기존 딥러닝 모델은 해석 가능성이 낮아 산업 현장에서 활용이 제한적이었으나, MILP를 통해 수학적으로 검증 가능한 해를 제공함으로써 투명하고 신뢰도 높은 결과 도출이 가능함. · 이는 고위험 산업군에서 신뢰성 기반 의사결정 체계 강화에 기여함.
3. 산학연 융합 최적화 인프라 확대 및 전문 인력 양성 기반 제공 · 본 기술은 수학 최적화, 기계학습, 공정공학 등 다학제 융합이 요구되는 기술로, 관련 분야 고급 전문 인력의 교육 및 양성에 기여 가능. · 최적화 알고리즘 개발, AI 기반 솔버 기술, 공정 제어 시스템 등 파생 산업의 활성화 또한 기대됨.
기술개발 일정 및 추진체계
개발 일정
구성원 및 추진체계
◇ ReLU 함수를 이용한 인공신경망 최신 연구 동향 조사 – 전원 인공지능/머신러닝 분야에 이용되는 ReLU 활성화 함수의 특성을 조사하고 ReLU 활성화 함수를 포함한 인공신경망을 다룬 논문을 분석하는 일련의 과정으로 최적화 분야에 대한 최신 연구 동향을 파악한다.
◇ 신경망 훈련 방법 조사 및 시뮬레이션 – 전원
인공신경망의 파라미터들을 최적화시키는 과정에 적용할 수 있는 코드를 조사하고 이를 바탕으로 간단한 모델을 만들어 PyTorch에 적용한다.
◇ 신경망 훈련 단계에서 적용 가능한 OBBT / Scaling ReLU 방법 시뮬레이션 – 이창형, 이학균
신경망 훈련 단계에서 OBBT / Scaling ReLU 방법에 대한 시뮬레이션을 진행하여 각 방법의 성능, 효율성을 평가한다.
◇ 신경망 훈련 후 적용 가능한 Clipped ReLU activation, Dropout, L1 Regularization 시뮬레이션 – 박근영, 진주희
신경망 훈련 단계를 거친 후 실행하는 최적화 과정에서 계산 효율성을 향상시킬 수 있는 Clipped ReLU activation / Dropout / L1 정규화 총 3가지 방법에 대한 시뮬레이션을 진행하여 각 방법의 성능, 효율성을 평가한다.
◇ 최종 최적화 방법 제시 - 전원
총 5가지 방법으로 시뮬레이션한 결과를 종합하여 최적의 신경망을 설계하고 실제 데이터를 이용해 최적화 과정을 실행해 성능, 효율성 측면을 비교한다.
설계
공정 모델 정의 및 데이터 수집
본 연구는 인공신경망이 내장된 MILP(Mixed-Integer Linear Programming) 문제의 계산 효율을 높이고, 이를 실제 산업 공정(수소 생산 시스템)에 적용하여 최적화하는 것을 목표로 한다. 이를 달성하기 위해 아래와 같은 절차로 실험 및 설계를 수행하였다.
① 공정 구성 개요 본 연구에서 최적화를 적용한 시스템은 CH₄(메탄)과 CLS(Chemical Looping System) 기반의 수소 생산 공정이다. Yang et al. (2021)의 “Thermodynamic analysis of chemical looping coupling process for coproducing syngas and hydrogen with in situ CO₂ utilization” 논문을 참고하였다. 해당 공정은 다음과 같은 다단계 반응 및 분리 장치들로 구성된다.
FCR (Fuel Combustion Reactor) FRR (Feed Reforming Reactor) CSR (CO Shift Reactor) SR (Separator Reactor) SEP-101~105 (Separator Units) AR (Air Separation Unit)
해당 공정은 재순환이 없는 단방향 흐름(non-recycle structure)을 기반으로 하며, 전체 흐름의 최종 목적은 H₂와 N₂의 분리 및 고순도 수소, SYNGAS 생산 최적화이다. 이 공정에서 발생하는 SYNGAS의 H/CO 비율을 2로 조정하면 고순도 수소(100% purity)와 고순도 SYNGAS(99% & 93% purity)를 얻을 수 있다.
② 입력 변수 (Design Variables) 총 10개의 연속적인 설계 변수를 사용하며, 각 반응기의 feed ratio와 온도를 포함한다.
③ 출력 변수 SEP-102, SEP-103, SEP-104에서 최종 생성되는 SYNGAS-1, SYNGAS-2, 수소(H₂)에 있는 CO와 H의 합을 출력 변수로 사용하였다. SYNGAS-1, SYNGAS-2의 H/CO 생산 비율이 2가 되도록 제약을 두고 얻은 데이터를 출력 변수로 사용하며, 이는 최적화의 목표 함수로 활용된다. 즉, output을 최대로 만드는 조건을 찾으면 H 생산을 최대로 만들 수 있다.
Surrogate 모델 설계 및 학습
복잡한 화학공정의 거동을 정확히 파악하기 위해서는 고정밀 시뮬레이션이 요구되지만, 이로 인한 계산 비용이 매우 클 수 있다. 이에 따라 본 연구에서는 공정 데이터를 기반으로 다층 퍼셉트론(Multi-Layer Perceptron, MLP)을 활용한 대리모델(surrogate model)을 설계하고 학습하여, 실제 공정의 반응을 근사하는 방식으로 계산 효율을 높이고자 하였다.
① 모델 구조 입력: 위의 10개 연속 설계 변수 출력: SYNGAS-1,2와 H output에 포함된 CO와 H의 유량 모델 형태: 다층 퍼셉트론(MLP, Multi-Layer Perceptron) 활성화 함수: ReLU
MLP는 입력층과 출력층 사이에 하나 이상의 은닉층을 가진 인공신경망 구조이며, 각 층의 뉴런은 이전 층의 출력값에 대해 선형변환을 수행한 뒤 비선형 활성화 함수를 적용하여 다음 층으로 전달한다. 본 연구에서는 모든 은닉층에 ReLU(Rectified Linear Unit) 함수를 활성화 함수로 사용하였다. ReLU는 입력값이 0 이하일 경우 0을 출력하고, 0보다 클 경우 해당 값을 그대로 출력하는 함수로, 다음과 같이 정의된다.
이를 통해 모델이 비선형성을 표현하면서도 학습 및 최적화 과정에서 계산 효율을 유지할 수 있다.
② 정규화 및 정칙화 기법 모델의 입력은 10개의 연속형 설계 변수이며, 출력은 수소(H₂) 생성량으로 설정하였다. 모델 학습 시, 입력과 출력 모두 [0,1] 구간으로 정규화하여 각 변수의 스케일 차이로 인한 학습 불균형을 방지하였다. 또한, 과적합(overfitting)을 방지하고 일반화 성능을 향상시키기 위해 L1 정규화와 Dropout 기법, Scaling 을 함께 적용하였다.
(1) L1 정규화 L1 정규화는 가중치 벡터의 절댓값 합에 패널티를 부여하여 불필요한 뉴런을 억제하고, 모델을 더 간결하게 만들어준다. 이를 수식으로 나타내면 다음과 같다.
(2) Dropout
Dropout은 학습 과정에서 무작위로 일부 뉴런을 비활성화하여 뉴런 간의 공동작용(co-adaptation)을 줄이고, 보다 일반화된 표현을 학습하도록 유도하는 기법이다. 다만, Dropout은 최적화 관점에서 신경망의 복잡도를 증가시킬 수 있어 적용 비율에 유의할 필요가 있다.
(3) Scaling 입력 및 출력 데이터는 각 데이터의 평균과 표준편차를 이용하여 직접 정규화 처리를 진행했다. 입력 변수들이 서로 다른 스케일을 가지고, 범위도 다르기 때문에 높은 차원의 모델 학습 시 안정하지 않고 수렴 속도가 느릴 수 있다. 이를 방지하기 위해 각 변수에 대해 스케일 차이를 제거하는 직접 정규화 Scaling 방식을 사용했고, 이로 학습 시 수렴 속도와 정확도를 개선할 수 있다. ③ 학습 조건 Loss: MSE (Mean Squared Error) Optimizer: Adam Epochs: 1000 이상 조기 종료(Early stopping) 및 MAE 기준 평가 병행 모델 학습에는 평균제곱오차(MSE)를 손실 함수로 사용하였고, Adam 옵티마이저를 활용하여 학습을 수행하였다. 학습은 1000 epoch 이상으로 설정하되, 조기 종료(Early stopping) 조건을 추가하여 과적합이 발생하지 않도록 하였다. 모델 성능 평가는 평균절대오차(MAE)와 결정계수(R² score)를 병행하여 실시하였다.
MILP 문제 구성 및 변환 학습된 신경망을 기반으로 혼합정수선형계획(MILP: Mixed-Integer Linear Programming) 형태의 최적화 문제를 구성하였다. 최적화의 목적은 수소 생성량을 최대화하는 것이며, surrogate 모델의 출력값을 MILP의 목적 함수로 사용한다. 신경망의 출력은 여러 개의 은닉층을 거치며 연속적으로 구성된 ReLU 연산의 결과이므로, 수학적으로는 부분구간별 선형(piecewise-linear) 함수로 표현 가능하다. 이를 MILP 형식으로 변환하기 위해 각 뉴런의 활성 상태를 이진 변수로 도입하고, ReLU 함수를 선형식으로 분해하여 다음과 같은 형태로 모델링한다.
뉴런의 전활성값에 대한 하한 및 상한을 지정한다. 이러한 방식은 ReLU의 비선형성을 선형 제약식과 이진 변수의 조합으로 표현할 수 있게 해준다. 하지만 이 방식은 ReLU마다 이진 변수를 하나씩 추가하게 되어 계산량이 급격히 증가하고, Big-M 계수의 크기가 최적화 성능에 결정적 영향을 미친다. 따라서 본 연구에서는 3가지의 경계 설정 기법을 통해 Big-M 계수를 개선하고 MILP 문제의 계산 효율을 향상시켰다.
실험 조건 및 시나리오
본 연구에서는 복잡한 화학 공정 데이터를 기반으로 학습한 신경망 surrogate 모델을 MILP 형태로 변환하고, 그 위에 다양한 경계 설정 기법을 적용하여 최적화 성능을 비교하였다. 비교 대상은 총 세 가지 시나리오로 구성되며, 각각 No Bound, FBBT(Feasibility-Based Bound Tightening), OBBT(Optimization-Based Bound Tightening) 기법을 적용한 경우이다. 모든 실험은 동일한 네트워크 구조 및 입력 조건 하에서 수행되며, 최적화 목적은 수소 생성량(H₂)의 최대화이다. 비교 지표로는 Gurobi solver의 계산 시간, 수렴 여부, 그리고 stable neuron 비율이 사용되었다.
(1) No Bound 가장 단순한 경계 설정 방식으로, 각 뉴런의 전활성값(pre-activation)에 대해 명시적인 상하한을 부여하지 않는다. 이 경우 MILP 모델에서는 Big-M 방식이 적용되지만, 경계가 존재하지 않아 solver는 극단적으로 큰 M 값을 자동으로 추론하여 사용하게 된다.
(2) FBBT(Feasibility-Based Bound Tightening) FBBT는 Pyomo 최적화 모델에서 사용되는 자동 경계 조정 기법으로, 모델의 수학적 구조만을 기반으로 각 변수에 대해 현실적으로 가능한 값의 범위를 계산하고 전파(propagate)하는 방식이다. 이 기법은 선형 및 비선형 제약 조건, 신경망의 계층 구조, 활성화 함수의 수식 등을 따라 변수 간의 연산 관계를 해석하고, 이를 통해 입력으로 주어진 bound로부터 각 중간 변수(특히 뉴런의 pre-activation 값)의 상하한을 순차적으로 계산한다. 이러한 경계 전파는 다음과 같은 구간 산술(Interval Arithmetic, IA) 규칙을 따른다. 예를 들어, 뉴런 𝑖의 𝑘-번째 계층 전활성값의 하한 및 상한은 다음과 같이 계산된다.
FBBT는 모든 경계를 한 번에 전체 모델 구조를 따라 자동 계산하기 때문에 계산 속도가 매우 빠르며, 별도의 최적화 문제를 풀지 않아도 되는 장점이 있다. 특히 Pyomo 및 OMLT와 같은 최적화 도구에서는 신경망을 MILP로 변환할 때 FBBT가 기본적으로 적용된다.
그러나 이 방식은 변수 간의 상관관계(correlation)나 글로벌 의존성(global dependency)는 반영하지 못한다. 예를 들어, 여러 개의 뉴런이 동시에 활성화될 수 없거나 비활성화되어야 하는 구조적 제약이 있는 경우, FBBT는 이를 고려하지 못하고 경계를 다소 보수적으로 계산(overestimated bound)할 수 있다. 이러한 한계로 인해 Big-M 계수는 감소하지만, OBBT에 비해 그 폭은 크지 않다.
(3) 선형계획 기반 OBBT (LP-based Optimization-Based Bound Tightening) OBBT는 각 뉴런의 전활성값(pre-activation)에 대해 가능한 최소값과 최대값을 직접 계산하기 위해, 해당 뉴런의 출력을 목적함수로 하는 선형계획 문제(LP)를 설정하고 이를 최적화하는 방식이다. 이 과정에서 전체 신경망은 MILP 형식으로 정식화되며, ReLU 함수는 Big-M 기법을 사용하여 이진 변수와 연속 변수로 표현된다. 예를 들어, 뉴런 𝑘의 전활성값을 라 할 때, OBBT는 다음과 같은 목적함수 하의 최소화 문제를 푼다.
해당 문제는 전체 ANN의 Big-M 기반 MILP 제약 조건을 그대로 유지한 상태에서, 특정 뉴런의 pre-activation 값을 최소화(또는 최대화)하는 구조로 구성된다. ReLU의 MILP 표현에는 다음과 같은 핵심 제약식이 포함된다.
이러한 LP 문제를 각 뉴런마다 두 번씩 반복적으로 풀어야 하므로 계산량은 크지만, 결과적으로 Big-M 계수를 효과적으로 줄이고 안정적인 경계 값을 얻을 수 있다. 참고한 선행연구 논문에서는 OBBT 적용 시 다음과 같은 성능 개선이 관찰되었다. 평균 Big-M 계수: 약 54% 감소 Stable neuron 비율: 약 5.5%p 증가 Gurobi 계산 시간: 평균 43% 단축
따라서 OBBT는 높은 정밀도가 요구되는 MILP 최적화 문제에서 매우 유효한 기법이며, 본 연구에서는 이를 기반으로 실험을 구성하고 경계 설정 전략의 효과를 정량적으로 분석하였다.
실제 공정에의 적용 및 최적 조건 도출 최종적으로, 위 실험을 통해 도출한 MILP 최적 조건은 CH₄ + CLS 공정의 실제 운전 조건에 반영 가능한 형태로 제공된다. 실제 조건 범위 내에서 H₂ 생산량이 최대가 되는 지점 탐색 조건: 반응기의 온도/feed ratio 등 조절 가능한 10가지 변수 조합 surrogate 모델 기반 MILP 해석 결과는 단일 최적 조건 벡터로 산출되며, 공정 운영 설계에 즉시 반영 가능
전체 설계 흐름 요약 1. 공정 모델링 및 입력/출력 변수 정의 2. 시뮬레이션을 통한 공정 데이터 수집 3. MLP surrogate 모델 설계 및 학습 (ReLU 기반) 4. MILP 구조로 변환 (binary 변수, Big-M 기법 적용) 5. Bound Tightening 기법 (FBBT, OBBT) 적용 6. 최적화 수행 및 계산 효율성/정확도 평가 7. 최적 조건 해석 및 실제 공정 반영 가능성 검토
결과 및 평가
완료 작품의 소개
포스터
관련사업비 내역서
내용
완료작품의 평가
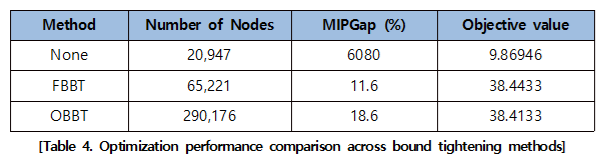
실제 공정 데이터를 대상으로 한 이번 최적화 실험 결과를 분석한 결과, 노드 탐색 수는 OBBT > FBBT > None 순으로 나타나며, 정확도인 수렴도는 FBBT > OBBT > None 순으로 확인된다. 이러한 결과는 각 기법의 특성과 탐색 전략에서 기인한 것으로 볼 수 있다.
우선, OBBT는 각 변수의 경계를 정밀하게 조이기 위해 반복적인 선형계획 최적화를 수행함으로써, 이론적으로 가장 강력한 bound tightening 기법이다. 그러나 모든 변수에 대해 LP를 푸는 과정은 MILP 모델 자체를 복잡하게 만들고, Solver가 수행해야 할 탐색 노드 수를 크게 증가시키는 원인이 된다. 실제 실험에서도 OBBT는 가장 많은 탐색 노드를 기록했으며, 계산량 증가에 따른 수렴 지연으로 인해 MIPGap이 18.6%로 FBBT보다 높게 나타났다.
반면, FBBT는 모델의 구조와 제약식을 기반으로 변수 간 연산을 통해 경계를 전파하는 방식으로, 계산 비용이 매우 낮고 빠르게 경계를 수렴시킬 수 있다. 실험 결과 FBBT는 탐색 노드 수가 OBBT보다 4배 이상 적었음에도 불구하고 더 낮은 MIPGap(11.6%)과 더 높은 출력값(38.4433)을 달성하며, 전체적인 계산 효율성과 수렴 품질 면에서 가장 우수한 성능을 보였다.
None의 경우에는 Bound Tightening 기법을 전혀 적용하지 않은 상태로, 탐색 노드 수는 가장 적었지만 출력값이 9.86946으로 매우 낮았고, MIPGap이 6080%에 달해 해의 신뢰성을 확보할 수 없는 것으로 나타났다. 이는 Bound Tightening이 MILP 최적화에서 해의 품질과 수렴을 좌우하는 핵심 전처리 과정임을 시사한다.
따라서 이번 실험에서는 정확도와 계산 효율성 모두에서 FBBT > OBBT > None의 순위를 확인할 수 있었다. 이는 FBBT가 빠르고 효율적으로 변수의 경계를 좁힘으로써 MILP solver가 탐색 공간을 효과적으로 줄이고, 더 안정적으로 수렴할 수 있도록 해주었음을 의미한다. 반면, OBBT는 계산량이 많아 solver가 실질적인 해 탐색에 충분한 시간을 확보하지 못하는 구조적 한계를 드러냈다. 이와 같은 결과는 Bound Tightening 기법이 solver 탐색 메커니즘에 어떠한 영향을 미치는지를 실증적으로 보여주는 사례라 할 수 있다.
앞서 Bound Tightening 기법 비교를 통해 FBBT의 구조적 간결성과 계산 효율성, 그리고 실제 수렴 품질 측면에서의 우수성을 확인할 수 있었다. 그러나 이러한 결과에도 불구하고, OBBT가 갖는 이론적 강점 또한 무시할 수 없다. 특히 변수 간 상호작용이 복잡하거나 단순한 구간 산술 기반 전파로는 경계를 효과적으로 좁히기 어려운 상황에서는, FBBT만으로는 해의 품질이 급격히 저하되거나 수렴 자체가 실패할 수 있다. 이는 비선형성이 내포된 surrogate 모델이나, 탐색 공간이 넓어 solver가 잘못된 방향으로 가지(branch)를 확장할 가능성이 높은 모델에서 특히 두드러진다.
OBBT는 각 변수의 bound를 선형계획 문제를 통해 직접 계산함으로써, 변수 간의 의존성과 제약 조건을 정밀하게 반영할 수 있다. 이를 통해 과도하게 넓은 bound로 인해 발생할 수 있는 계산량 폭증 및 수렴 실패 문제를 사전에 억제하는 데 효과적이다. 따라서 모델 전체에 일괄적으로 적용하기엔 계산 자원 부담이 크더라도, 전략적으로 특정 변수에만 적용하는 방식은 실질적인 이점을 제공할 수 있다.
이에 따라 민감도 기반 변수 영향도 분석을 통해 출력에 큰 영향을 미치는 변수를 구분하였다. 민감도가 높다고 분류된 v₀, v₅, v₆ 변수는 값의 조절 범위도 넓어 탐색 공간에서 차지하는 비중이 크며, solver의 가지치기(branch-and-bound) 과정에서 중요한 역할을 수행할 가능성이 높다. 따라서 모든 변수에 FBBT를 적용하되, v₀, v₅, v₆에 대해서만 부분적으로 OBBT로 처리하는 Hybrid Bound Tightening 전략을 추가적으로 진행하였다. 이 접근법은 계산 효율성과 해의 정밀도 간의 균형을 달성하기 위한 실용적 해법으로, MILP 기반 surrogate 최적화와 같이 계산 자원이 제한된 문제에서 유효한 적용 가능성을 제시한다.
부분적 OBBT 전략에 따른 결과
 이번 실험에서는 기존의 세 가지 Bound Tightening 전략(None, FBBT, OBBT)과 본 연구에서 제안한 부분적 OBBT 전략을 비교하여, 계산 효율성과 수렴 품질 측면에서의 상대적 성능을 정량적으로 분석하였다. 그 결과, 부분적 OBBT 전략이 MIPGap, 탐색 노드 수, 계산 시간, 목적함수 값 모든 지표에서 가장 우수한 성능을 보이며, 실용적 효용성을 입증하였다.
이번 실험에서는 기존의 세 가지 Bound Tightening 전략(None, FBBT, OBBT)과 본 연구에서 제안한 부분적 OBBT 전략을 비교하여, 계산 효율성과 수렴 품질 측면에서의 상대적 성능을 정량적으로 분석하였다. 그 결과, 부분적 OBBT 전략이 MIPGap, 탐색 노드 수, 계산 시간, 목적함수 값 모든 지표에서 가장 우수한 성능을 보이며, 실용적 효용성을 입증하였다.
먼저 수렴 품질 측면에서, 부분적 OBBT는 최종 MIPGap이 0.94%로, FBBT(11.6%)나 OBBT 전체 적용(18.6%)에 비해 현저히 낮은 값을 기록하였다. 이는 Solver가 최적해에 매우 근접한 해를 도출했음을 의미하며, 정밀한 Bound 설정이 부분적으로만 적용되어도 수렴 안정성에 매우 긍정적인 영향을 줄 수 있음을 시사한다. 특히, None 방식의 경우 MIPGap이 6080%에 달해 해의 신뢰성 자체가 확보되지 않았다는 점을 고려할 때, Bound Tightening의 중요성이 더욱 강조된다.
탐색 노드 수 측면에서도 부분적 OBBT는 97,043개의 노드를 탐색하며 수렴에 도달하였다. 이는 OBBT 전체 적용 방식의 절반 이하(290,176개) 수준이며, FBBT보다 약간 많지만 Solver의 탐색 효율 측면에서 균형 잡힌 성능을 보여준다. 이는 OBBT의 계산량 증가 문제를 해소하면서도, Solver가 주요 변수의 경계를 효과적으로 활용해 탐색 효율과 수렴 품질을 동시에 확보했음을 의미한다.
계산 시간은 더욱 주목할 만한 결과를 보였다. 기존 세 가지 기법(FBBT, OBBT, None)은 모두 계산 종료 제한 시간으로 설정한 7200초를 모두 소진했으나, 부분적 OBBT는 6104초 만에 계산을 성공적으로 완료하였다. 이는 약 1100초 이상 단축된 결과이며, 탐색 성능 향상에 따라 Solver가 빠르게 수렴 경로를 확보했음을 보여준다. 특히 복잡한 surrogate 기반 MILP 문제에서 제한 시간 내에 유효한 해를 도출하는 것은 실제 공정 최적화에서 중요한 요건으로 작용한다.
최적 출력값 측면에서도, 부분적 OBBT는 38.4968이라는 최고치를 기록하였다. 이는 FBBT(38.4433), OBBT(38.4133)보다 높은 결과이며, 계산 정확도와 해의 품질이 동시에 개선되었음을 의미한다. OBBT의 정밀한 Bound를 통한 탐색 안정성과 FBBT의 빠른 계산 특성이 적절히 결합된 전략이 가장 실용적인 최적화 성능을 달성할 수 있음을 보여주는 결과이다.
결과적으로, 변수 선택적으로 OBBT를 부분 적용하는 방식은 계산 비용과 수렴 품질 간의 Trade-off를 해소할 수 있는 유효한 개선 방안으로 평가된다. 특히 본 연구에서는 변수 v0, v5, v6가 최적화 과정에서 민감도가 높은 변수임을 확인하고, 해당 변수에 대해서만 OBBT를 수행하는 방식을 통해 solver가 보다 효율적인 탐색을 수행할 수 있도록 지원하였다. 이러한 접근법은 Bound Tightening 기법의 실용적 활용 측면에서 중요한 시사점을 제공한다.
뉴런 활성화 분석을 통한 최적화 경로 안정성 평가
ReLU 기반 신경망을 MILP로 변환하여 최적화에 활용할 경우, 각 뉴런의 활성화 상태(활성화 여부 이진 변수 𝑧)는 MILP 제약식의 형태로 반영된다. 이때 뉴런의 활성화가 안정적으로 0 또는 1로 고정될 경우 해당 뉴런은 ‘stable neuron’으로 간주되며, 반대로 활성화 상태가 문제 내에서 결정되지 않고 부동적인 경우는 ‘unstable neuron’으로 분류된다. 이는 MILP의 이진 변수 수, 곧 문제 복잡도에 직결되므로, 뉴런 반응의 안정성은 전체 최적화 성능과 밀접한 관련이 있다. 이번 실험에서는 OBBT 전체 적용 전략과 부분적 OBBT 전략(v₀, v₅, v₆ 변수에만 적용) 각각에 대해 뉴런 활성화 경로를 시각화하고 층별 반응을 비교하였다. 시각화 결과에 따르면, OBBT 전체 적용 시 대부분의 층에서 뉴런들의 평균 활성 값이 0과 1 사이에 고르게 분포하며, 많은 뉴런이 unstable한 상태에 머무른 것으로 나타났다. 이는 OBBT가 계산적으로 많은 경계를 정밀화했음에도 불구하고, 최적화 경로 상의 안정성을 확보하지 못했음을 시사한다. 반면, 부분적 OBBT 전략에서는 뉴런 반응의 경계가 더욱 뚜렷하게 나타났으며, 일부 뉴런은 완전히 stable한 0 또는 1로 고정되는 양상을 보였다. 특히 Layer 2~4에서 활성화 경계가 정돈되어 있으며, 불안정 뉴런의 수가 눈에 띄게 감소하였다. 이는 Solver가 주요 변수의 경계를 보다 정밀하게 파악한 상태에서, 전체 신경망을 더 안정적인 경로로 수렴시켰다는 것을 의미한다.
이러한 결과는 부분적 OBBT 전략이 단순히 계산량을 줄이는 데 그치지 않고, 실제 MILP 구조의 계산 안정성과 경로 예측 가능성 측면에서도 우수한 성능을 보였음을 시사한다. Stable neuron의 증가 현상은 MILP 모델에서 해당 뉴런의 이진 변수 제약이 제거될 수 있는 가능성을 의미하며, 이는 최적화 속도 개선뿐만 아니라 Solver의 가지치기 효율 향상에도 기여할 수 있다.
따라서 뉴런 반응의 시각적 비교 결과는 부분적 OBBT 전략이 구조적 계산 복잡도를 낮추고, MILP 기반 최적화 과정에서 효과적인 경로 안정화 수단으로 기능할 수 있음을 실증적으로 보여준다.
향후계획
본 연구는 딥러닝 기반 예측 모델을 포함하는 MILP(Mixed-Integer Linear Programming) 문제의 계산 효율을 향상시키기 위한 실용적인 전략을 제시하였으며, 다양한 학문 및 산업 분야에 폭넓게 기여할 수 있는 가능성을 가진다. 특히 ReLU 신경망을 MILP로 표현하는 구조는 유지하면서, 계산 자원을 절감할 수 있는 OBBT(Optimization-Based Bound Tightening) 기법의 적용은 다음과 같은 전망을 갖는다.
1) 머신러닝 기반 최적화의 실용화 기반 마련 딥러닝 모델을 포함한 최적화 문제는 계산량 증가로 인해 산업적 활용이 어려운 경우가 많았다. 본 연구에서 제안한 OBBT 기반 bound 최적화 전략은 MILP 내 신경망 구조를 그대로 유지하면서도 계산 효율을 높임으로써, 실제 응용이 가능한 수준으로 성능을 개선한다. 이 기술은 향후 설계 자동화, 스마트 제조, 실시간 제어 시스템 등 AI 기반 산업 응용에서 핵심 기반 기술로 기능할 수 있다.
2) 화학공학 공정 최적화 문제에의 응용 공정 모사 또는 실험 데이터를 기반으로 학습된 딥러닝 예측 모델을 공정 최적화 문제에 통합하려는 시도는 증가하고 있다. 본 연구의 접근은 계산 병목을 유발하지 않으면서도 신경망 기반 surrogate model을 활용한 공정 제어에 활용될 수 있어, 반응 조건 최적화, 원료 배합 최적화, 에너지 효율 향상 등 다양한 화학공정 분야에 직접 응용 가능하다.
3) 딥러닝 검증 기술 및 해석 가능성 기여 신뢰성과 안전성이 요구되는 분야에서 딥러닝 모델의 검증 가능성 확보는 필수적이다. 본 연구는 ReLU 기반 신경망의 MILP 표현을 계산적으로 실현 가능한 수준으로 단순화함으로써, 자율주행, 의료 AI, 항공우주 시스템 등의 안전성 검증에도 기여할 수 있다. 이는 신경망 검증을 위한 MILP 접근법의 산업 적용 가능성을 크게 넓히는 효과를 가진다.