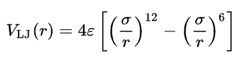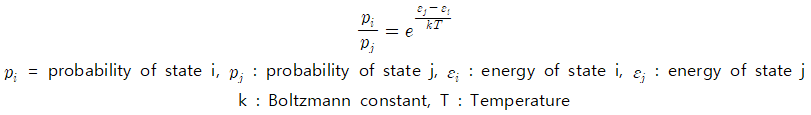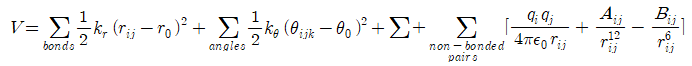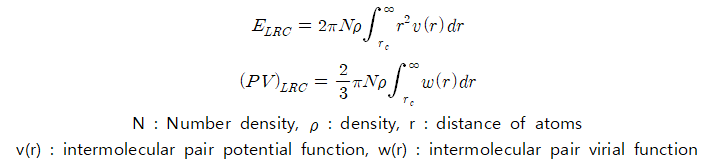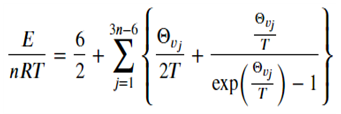"장재언1팀"의 두 판 사이의 차이
Adchem20220209 (토론 | 기여) (→완료 작품의 소개) |
Adchem20220209 (토론 | 기여) (→시뮬레이션 결과) |
||
| 199번째 줄: | 199번째 줄: | ||
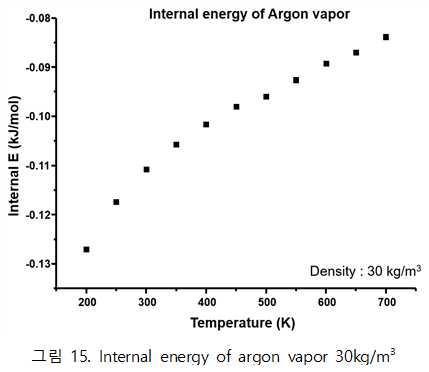
◇ NVT ensemble에서 Internal energy (비이상에너지) 값 도출 | ◇ NVT ensemble에서 Internal energy (비이상에너지) 값 도출 | ||
- Argon vapor | - Argon vapor | ||
| + | [[파일:InternalenergyofArgonvapor.PNG|가운데]] | ||
| + | |||
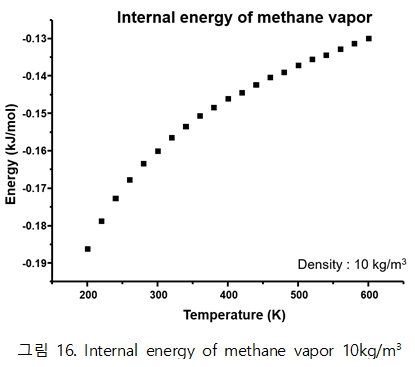
| + | - Methane vapor | ||
| + | [[파일:Internalenergyofmethanevapor.PNG|가운데]] | ||
| + | |||
| + | 그림 15, 16은 canonical ensemble 시스템에서 simulation을 통해 구한 열역학적 물성인 internal energy를 온도에 따라 나타낸 그래프다. Simulation을 통해 구한 비이상 internal energy를 직접적으로 NIST 실험값과 비교할 수 없다. 따라서 NIST에 기입되어 있는 Heat capacity(Cv)를 통해 간접적으로 비교할 계획이다. 이 때 통계열역학으로 구한 이상에너지에 대한 값도 필요하다. 이상에너지에 대해 구하는 방법은 차후에 다루도록 하겠다. | ||
| + | |||
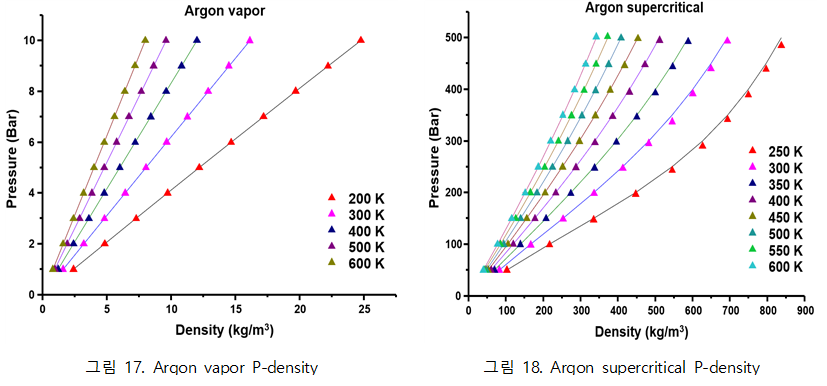
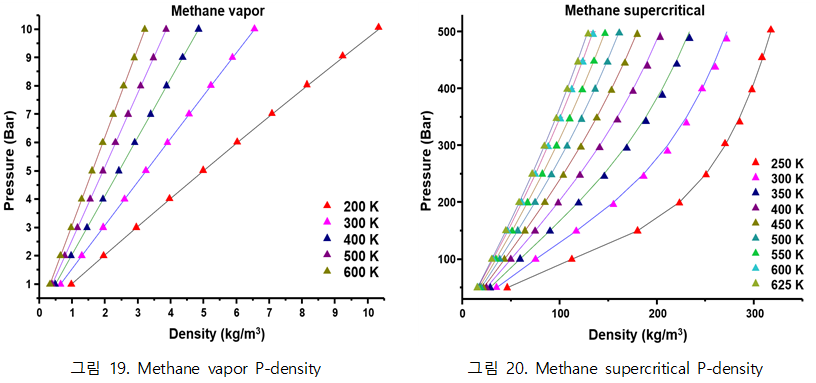
| + | ◇ NVT ensemble에서 Pressure 값 도출 ( P-density graph ) | ||
| + | Density 변화에 따른 Pressure를 각 물질에 따라 시뮬레이션 한 그래프. Isothermal system으로 설정하였으며, 실선은 NIST의 reference 값을 뜻하고 세모는 시뮬레이션 결과를 뜻한다. 즉, 선에서 벗어나지 않을수록 시뮬레이션 결과가 정확함을 뜻한다. | ||
| + | - Argon vapor, supercritical phase | ||
| + | [[파일:argon결과.PNG|가운데]] | ||
| + | |||
| + | - Methane vapor, supercritical phase | ||
| + | [[파일:methane결과.PNG|가운데]] | ||
| + | |||
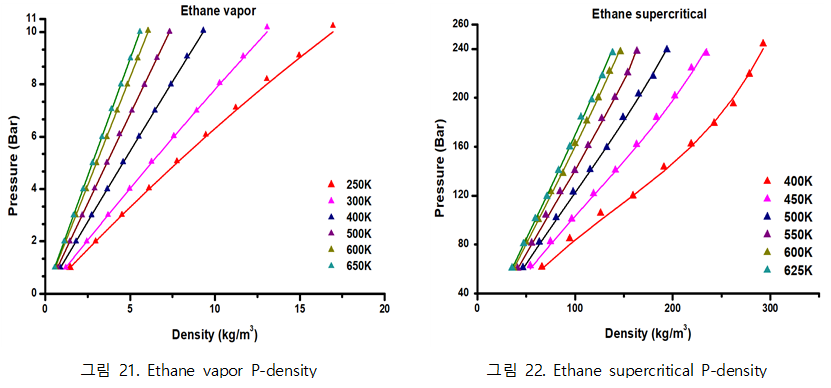
| + | - Ethane vapor, supercritical phase | ||
| + | [[파일:ethane결과.PNG|가운데]] | ||
| + | |||
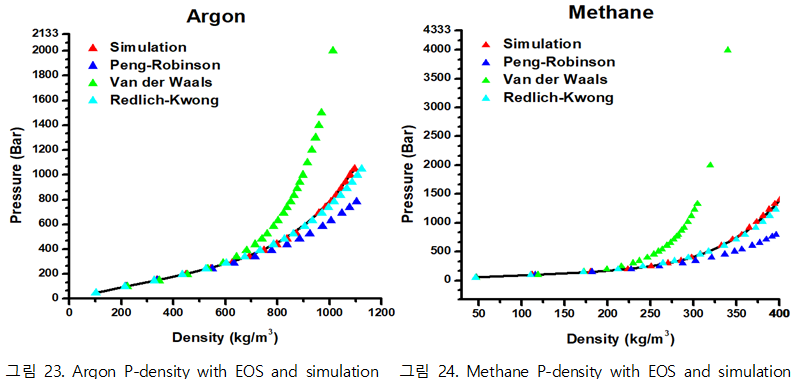
| + | ◇ 기존의 다양한 상태방정식과 Simulation의 정확도 비교 | ||
| + | - Comparison with Equation of State and simulation | ||
| + | [[파일:argon_methane_eos비교.PNG|가운데]] | ||
| + | |||
| + | 그림 23, 24는 Simulation이 기존 상태방정식보다 정확하게 예측하는지 비교하기 위한 그래프다. 각각 Argon과 Methane의 P vs density graph에서 검은색 선은 NIST 실험값이고 빨간색 삼각형은 simulation으로 구한 압력 값이며 나머지 색의 삼각형들은 기존 상태방정식에서 도출된 값을 뜻한다. 그래프를 통해 Argon, Methane 둘 다 상태방정식과 simulation이 밀도가 작은 영역에서는 NIST 값과 일치하는 경향성을 보였으나 밀도가 큰 구간에서 서서히 오차가 생기는 경향성이 보이는 것을 알 수 있다. 그 중 Van der Waals 상태방정식이 가장 부정확하게 압력 값을 예측하고 있고 그 다음은 Peng-Robinson 상태방정식이 NIST값과 큰 오차를 보이고 있다. 반면 Redlich-Kwong 상태방정식은 NIST값과 근사한 경향성을 보였으나 simulation보다 상대적으로 부정확한 값을 나타냄을 알 수 있다. 따라서 밀도가 큰 구간은 본 연구로 구현한 simulation이 타 상태방정식보다 정확하게 열역학적인 물성을 예측하고 있다는 것을 알 수 있다. | ||
| + | |||
| + | ◇ 시뮬레이션으로 계산한 Internal energy에 통계열역학적 이상에너지를 더하고 dU = CvdT 식을 이용해 각 물질의 Cv를 도출 | ||
| + | 위의 internal energy에 더해주는 통계열역학적 이상에너지 식은 단원자 분자인 Argon은 . 그 외의 methane이나 ethane의 경우 polyatomic ideal gas이므로 다음과 같은 식으로 계산한다. | ||
| + | [[파일:통계열역학에너지.PNG|가운데]] | ||
| + | |||
| + | 계산된 전체 에너지를 T에 대해 플랏한 후, 각 온도에서의 기울기를 통해 Cv값을 도출해낼 수 있다. | ||
| + | |||
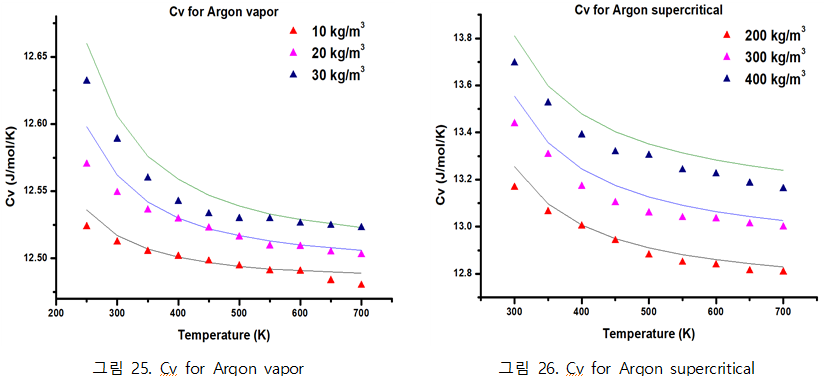
| + | - Argon vapor, supercritical phase | ||
| + | [[파일:argonCv.PNG|가운데]] | ||
| + | |||
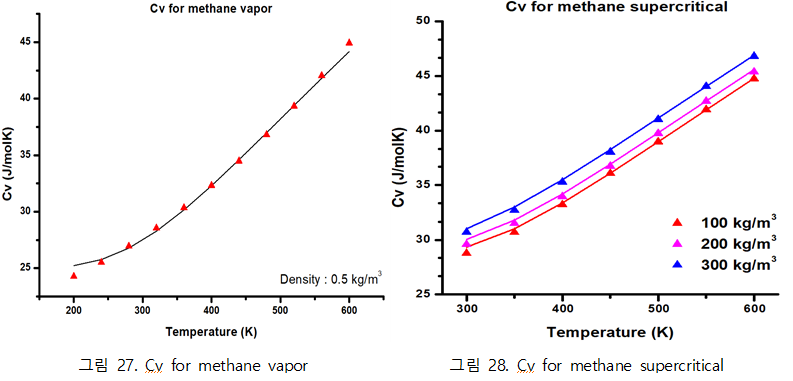
| + | - Methane vapor, supercritical phase | ||
| + | [[파일:methaneCv.PNG|가운데]] | ||
| + | |||
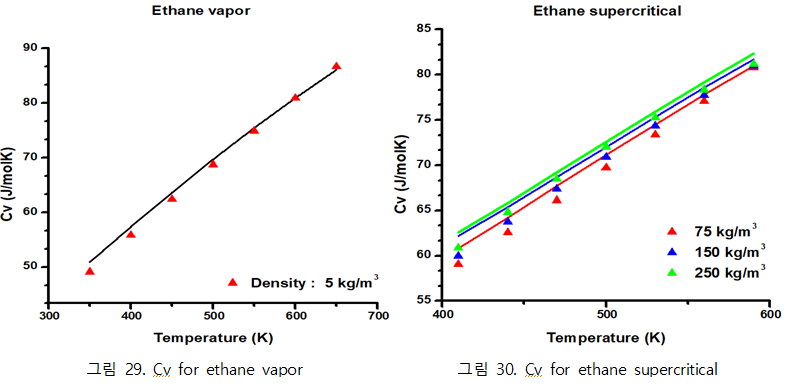
| + | - Ethane vapor, supercritical phase | ||
| + | [[파일:ethaneCv.PNG|가운데]] | ||
| + | |||
| + | =====정확도 분석 및 오차 경향성을 보기 위한 상대오차 그래프===== | ||
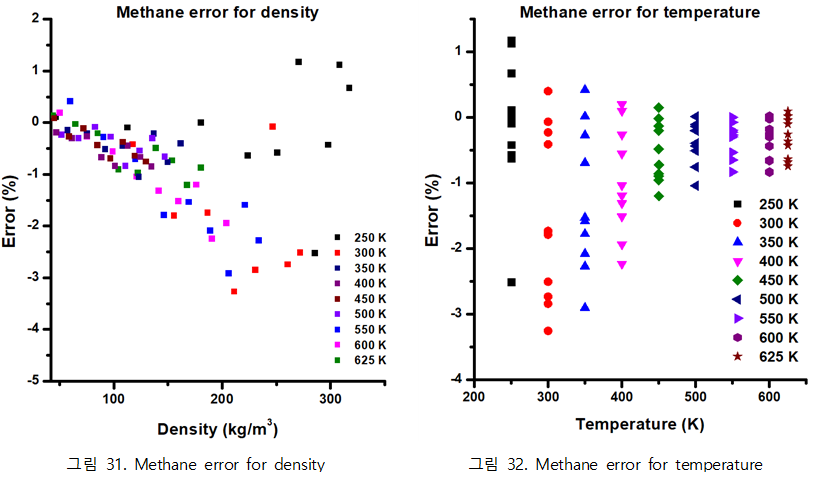
| + | [[파일:오차그래프.PNG|가운데]] | ||
| + | 그림 31를 보면 density가 300kg/m3으로 커질수록 상대오차가 크게 나옴을 알 수 있었다. 또한 그림 32에서 온도가 625K으로 커질수록 상대오차가 작게 나옴을 알 수 있었다. 즉, 상대오차는 시스템의 온도가 낮고 밀도가 커질수록 증가한다는 사실을 알 수 있었다. | ||
====프로토타입 사진 혹은 작동 장면==== | ====프로토타입 사진 혹은 작동 장면==== | ||
2022년 12월 9일 (금) 22:17 판
프로젝트 개요
기술개발 과제
국문 : 파이썬 환경에서 몬테카를로 알고리즘을 이용한 아르곤, 메테인, 에테인의 분자 시뮬레이션
영문 : Molecular simulation of Argon, Methane, Ethane with Monte Carlo algorithm in Python
과제 팀명
장재언 1팀
지도교수
장재언 교수님
개발기간
2022년 9월 ~ 2022년 12월 (총 4개월)
구성원 소개
서울시립대학교 화학공학과 2017340042 정성민(팀장)
서울시립대학교 화학공학과 2017340009 김정인
서울시립대학교 화학공학과 2017340037 이종범
서울시립대학교 화학공학과 2017340047 최영근
서론
개발 과제의 개요
개발 과제 요약
◇ 몬테카를로 알고리즘을 파이썬 환경에서 구현
◇ 분자 시뮬레이션을 위한 몬테카를로 코드 작성
◇ 기존 EOS로 예측이 어려운 분자들에 대한 물성 예측
◇ 실험결과와 시뮬레이션 결과 비교
◇ 프로그램 편의성을 개선시키기 위한 GUI개발
개발 과제의 배경
◇ 여러 제한적인 물질에만 쓸 수 있는 EOS과 다른 통계열역학 관점의 분자 시뮬레이션 - 분자의 구조 및 분자간 힘과 같은 미시적 특성으로부터 거시적인 열역학적 물성을 계산하는 방법으로 분자 시뮬레이션 중 몬테-카를로 방법을 사용하여 열역학적 물성을 구한다.
- 기존에는 유기화합물의 열역학적 물성을 알기위해 여러 상태방정식을 이용했다. 흔히 알려진 상태방정식인 SRK(Soave-Redlich-Kwong), PR(Peng-Robinson) 상태방정식은 극성이 있는 분자들에 대한 열역학적 물성에 정확한 예측이 힘들다는 단점이 있다.
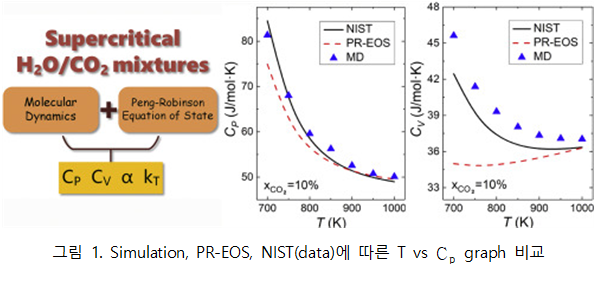
- CO2/H2O mixture의 열역학적 물성인 heat capacity를 molecular simulation과 PR-EOS로 구한 데이터를 비교한 선행연구를 참고하였다.
그림 1은 CO2/H2O mixture에서 NIST, PR-EOS, molecular simulation에 해당하는 heat capacity를 값을 각각 나타낸 그림이다. 위 그림을 통해 PR-EOS에 비해 molecular simulation의 값이 더 정확한 값을 가지는 것을 알 수 있다. 그 이유는 다음과 같다.
CO2/H2O mixture는 의 분율이 낮을수록 water의 수소결합의 효과로 극성이 높아진다. 해당 데이터는 CO2 분율 0.1에서 구한 그래프로, 이는 해당 화합물이 극성의 특성을 가지는 것을 의미한다. PR-EOS는 극성을 띄는 분자들에 대해 정확한 값을 표현하지 못하는 물질 의존적인 특성을 가진다. 이는 attractive force를 나타내는 alpha function이 극성 물질에 대한 증기압을 정확하게 나타내지 못하기 때문이다. Forero, L. A., & Velásquez, J. A. (2016). A generalized cubic equation of state for non-polar and polar substances. Fluid Phase Equilibria, 418, 74-87.
따라서 실험적으로 증명된 극성 물질의 data가 존재하지 않으면 EOS를 적용하기에 부정확하다. 따라서 위와 같이 극성을 갖는 mixture에 대해 molecular simulation을 사용하여 열역학적인 물성을 구하면 EOS 방법보다 정확한 값을 구할 수 있다.
◇ 대중성이 있는 파이썬을 사용하여 Molecular simulation 접근성 향상 - 보안성이 뛰어나 서버 특화 운영체제로 사용하는 유닉스 환경에서 텍스트 기반의 명령어인 스크립트 제어를 통해 분자 시뮬레이션 프로그램들을 구동한다. 유닉스 환경에서 구축해야한다는 점과 사용법을 익히기 어렵다는 점을 고려하면 비전문가나 연구자들이 분자 시뮬레이션 프로그램에 쉽게 접근할 수 없는 기존의 어려움이 있다. 대부분의 분자 시뮬레이션 프로그램은 유닉스 운영체제로 구동하지만 이외로 윈도우 운영체제에서 구동할 수 있는 대표적인 소프트웨어로 insilico 기업의 Material Studio가 있다. 현재 사용자들이 이용하고 있는 컴퓨터들의 운영체제가 대부분 윈도우 인 것을 고려하면 Material Studio 프로그램의 접근성이 다른 유닉스 기반 프로그램보다 훨씬 뛰어나다. 하지만 위 프로그램은 가격이 너무 비싼(약 2500만원) 치명적인 단점이 있다. 따라서 윈도우 운영체제에서 구동할 수 있어 접근성이 뛰어나고 대중성이 뛰어난 파이썬 기반의 Molecular simulation을 개발한다.
개발 과제의 목표 및 내용
◇ 파이썬 환경에서 몬테카를로 알고리즘을 이용한 분자 시뮬레이션 구현 - 분자 시뮬레이션 기법에 익숙하지 않은 이용자들이 쉽게 접근할 수 있으며 다양한 분자들에 적용할 수 있는 소프트웨어를 개발한다. 개발한 코드를 오픈소스로 공유함으로써 통계열역학이 익숙하지 않은 사람들이나, 통계열역학에 익숙하지만 파이썬으로 구현하지 못하는 사람들이 보고 참고할 수 있게 하여 추후에 진행될 연구에 도움이 될 수 있다.
◇ 몬테카를로 알고리즘 - 기계적인 절차에 따라 문제를 해결하는 과정을 나타내는 알고리즘과 달리 몬테카를로 시뮬레이션은 무작위성을 이용하여 문제를 해결하는 방법이다. 임의적으로 난수 값을 발생하여 많은 시뮬레이션을 통해 통계적인 분포에 따른 결과 값을 얻을 수 있다. 대표적인 예로 원주율을 구하는 방법이 있다. 길이가 1인 정사각형 안에 사분원이 그려진 시스템이 있다고 가정하자. 그 정사각형 안에 무작위의 점을 찍고 사분원안의 점의 수를 전체 찍은 점의 수로 나누는 일련의 과정을 실행한다. 전체 점의 개수가 적은 초기에는 시분원의 넓이인 와 무작위 점을 통한 실험값이 큰 차이를 보이지만 무수히 많은 점을 찍으면 그 값은 에 수렴하게 된다. 위와 같은 원리를 분자의 열역학적인 물성을 도출할 수 있는 시뮬레이션을 구현하는 것이 목표다.
- 몬테카를로 시뮬레이션 후 열역학적인 물성을 도출하기 위해서 앙상블에 대한 기본적인 지식이 필요하다. 앙상블의 경우 거시적인 세계에서의 열평형 상태에서도 미시적인 관점에서는 입자의 위치나 운동량 등이 수시로 변하게 된다. 이런 미시적인 상태를 거시적 세계의 복사본으로 볼 수 있는데, 이러한 입자들의 계의 모임을 앙상블이라고 한다. 앙상블에는 기본적으로 3가지가 존재한다. 고립계의 microcanonical ensemble 닫힌계의 canonical ensemble, 그리고 열린계의 grandcanonical ensemble이다. microcanonical의 경우 가장 기본이 되는 앙상블로 N, V, E를 일정하게 유지시키고 측정하는 방법이다. 이 경우 열역학적 수치를 측정할 수 있지만 서로 상호작용을 하지 않는 조건 하에 작동하는 시뮬레이션이기에 현실에서 에너지를 유지시키는 것은 어려워 적용할 수 없다. 이를 해결하기 위한 것이 canonical ensemble이다. 위치를 변화시킨 후 N, V, T를 일정하게 유지시켜 측정하는 방법이다. 매우 큰 capacitor를 가지고 있다고 가정할 경우 현실에 적용시킬 수 있어 온도를 일정하게 유지하는 조건을 만족할 수 있다. 그렇기에 이론상 허용되는 모든 수치를 가질 수 있는 장점이 있다. Canonical ensemble의 경우 입자의 개수가 정해져있어 입자의 개수가 변하는 경우를 측정하기 어렵다. 이를 해결한 방법이 grandcanonical ensemble이다. 열린계에서 사용할 수 있는 grandcanonical ensemble은 입자의 출입도 허용하기에 입자의 변화에 따른 열역학적 수치변화를 볼 수 있다. 이를 사용하기 위해서는 chemical potential을 일정하게 유지하는 조건으로 계산할 수 있다. 본 과제에서 canonical ensemble을 사용하여 열역학적 물성을 도출할 것이다.
- 몬테카를로 canonical ensemble을 이용해 분자의 열역학적 특성을 나타내는 과정은 다음과 같다.
- 몬테카를로의 무작위성을 각 분자의 위치에 적용한다. 초기에 물질의 고유한 값인 과 를 force field 데이터베이스에서 불러온다. 이 후 모든 분자의 위치를 랜덤하게 설정하고, 임의적으로 분자를 선택하여 위치를 무작위로 변화시킨다. 이 과정에서 변화한 포텐셜 에너지와 기존 상태의 포텐셜 에너지를 비교하며, 각 위치에서의 포텐셜 에너지는 다음 식을 통해 계산한다.
- 이를 비교하여 기존 포텐셜 에너지보다 새로운 포텐셜 에너지가 작을 경우 system은 새로운 포텐셜 에너지를 받아들이며 configuration 또한 새롭게 바뀐다. 하지만 새로운 포텐셜 에너지의 값이 큰 경우에는 볼츠만 분포의 확률 식에 따라 확률적으로 이를 받아들인다. 위 과정을 무수히 반복하면 분자들의 분포는 볼츠만 분포를 따르게 된다. 시뮬레이션 결과로 포텐셜 에너지를 구할 수 있고, 비리얼의 평균값을 통해 내부압력을 얻을 수 있다.
◇ Python pyqt 라이브러리를 이용해 시뮬레이션 결과를 구현 - 3차원 공간에 좌표축을 만들고 1개의 step마다 해당하는 시뮬레이션의 결과 값을 list형태로 받는다. 이 후 molecule의 반지름을 고려하여 분자 모델링을 거친 뒤 list에서 각각의 x,y,z좌표를 추출하여 3차원 공간에 표시한다. 위 과정을 cycle마다 반복하여 시뮬레이션 결과 값을 나타낸다.
◇ CPU Time을 최소화하고 Simulation data의 신뢰성을 향상 - 몬테카를로 시뮬레이션은 시행횟수가 증가할수록 정확도가 증가한다. 수백 개의 분자와 그 분자들 간 거리를 구하는 식, 구한 거리를 이용하여 포텐셜 에너지 식을 사용하는 환경에서 반복문을 이용하여 반복 횟수를 매우 높게 설정하여 시행횟수를 높이는 것은 결과까지 도출하는 것에 매우 높은 CPU Time이 요구된다. 따라서 코드를 최적화하여 CPU time을 줄일 수 있는 방법들을 고안한다.
관련 기술의 현황
관련 기술의 현황 및 분석(State of art)
- 전 세계적인 기술현황
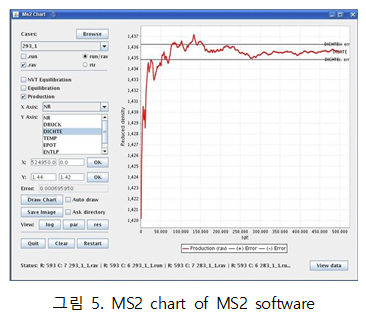
◇ MS2
- Fortran으로 작성되어 Unix / Linux 또는 Fortran Compiler 기반으로 돌아가며 사용하는 method의 예로 MD, MC, classical ensemble (canonical 포함), Green-Kubo formalism 등이 있다.
- 시뮬레이션 결과를 “ms2molecules”와 연동해 configuration을 시각적으로 나타낸다. 이를 통해 molecular trajectories(분자의 이동경로)를 나타내는 기능을 지원하고 molecule의 크기와 색을 이용자가 원하는 대로 바꿀 수 있다. 이를 통해 mixture의 거동을 나타내는 과정에서 solvent의 molecule 크기를 줄이는 방법을 통해 solute의 거동을 단독적으로 확인할 수 있다.
- 시뮬레이션 결과를 “ms2chart”와 연동할 수 있다. 그 역할은 시뮬레이션을 일시정지하고 재시작 할 수 있는 기능을 가지고 있으며 이는 cycle 수가 많은 경우 유리하게 작용한다. 그래프의 y축을 사용자가 직접 지정할 수 있어 관찰하고자 하는 항목에 대해 확인할 수 있으며 시뮬레이션 결과를 이미지 파일(.png)로 저할 수 있다는 장점이 있다.
◇ Materials Studio
- Visualizer라는 창을 통해 다양한 분자구조를 시각화한다. 부가적인 Builder의 기능으로 이용자가 클릭만으로 고분자중합체, 탄소나노튜브 같은 복잡한 분자구조를 Visualizer에 쉽게 구축할 수 있는 특징을 갖고 있다.
- 여러 모듈을 내장하고 그에 따른 기능을 제공한다. 기능의 예시로는 결정구조를 예측하는 모듈이 있다. 단결정 구조를 기반으로 결정을 예측할 수 있는 Morphology, 분자 구조를 기반으로 한 결정 구조를 예측할 수 있는 Polymorph Predictor, x-ray 데이터와 분자 구조를 기반으로 하여 결정 구조를 예측할 수 있는 Reflex를 제공한다. 이처럼 결정구조를 예측할 수 있는 모듈 외에도 다양한 모듈을 지원하는 특징을 가지고 있다.
- Simulation model의 크기에 따라 다양한 계산 방법을 제공한다. Model 크기가 에서 nm 범위의 전자 간 상호작용을 고려한 물성 예측의 경우는 quantum mechanics를 이용하여 분자의 밴드 구조, 기계적 성질 계산 등을 할 수 있다. nm에서 μm 범위인 경우는 molecular mechanics를 이용하고 이를 통해 표면에서 물리적 흡착, 이원 시스템의 혼합도 계산을 할 수 있다. 앞의 방법들은 원자단위를 통한 계산방법이며, 원자 여러 개를 하나의 segment로 보고 같은 계산해 같은 자원으로 더 큰 범위의 system을 계산할 수 있다. 위의 방법은 μm에서 mm의 system범위를 다루는 mesoscale modeling이다. 이를 통해 μm에서 mm의 시스템에서 phase의 형성, 접촉각, 표면장력 등을 다룰 수 있다. 이처럼 매우 작은 scale에서 여러 정보들을 얻을 수 있는 기능들을 제공한다.
- 특허조사
◇ 순수한 화합물의 물리화학적 및 열역학적 성질을 예측,프로세스 및 온라인 서비스하는 모델,방법 및 시스템
국제공개번호 : WO2012/177108 A3 발명자 : 성애리 특징 : 수소(H), 탄소(C), 질소(N), 산소(O), 황(S) 등 5가지 이내의 원소로 구성되고 수소를 제외한 원자의 개수가 25개 이하인 분자로 이루어진 순수한 유기화합물의 물리화학적 및 열역학적 물성을 예측하는 온라인 서비스 모델. 실험값이 알려지지 않은 조건의 유기화합물에 대해서도 값을 예측할 수 있다.
◇ SYSTEM AND METHOD FOR SIMULATING THE TIME-DEPENDENT BE HAVIOUR OF ATOMI AND/OR MOLECULAR SYSTEMS SUBJECT TO STATIC OR DYNAMIC FIELDS
국제공개번호 : US 2008/0147360 A1 발명자 : Anthony Peter Fejes, John Silvlo Vieceli, Shayan Rahnama, Ganesan Swaminathan 특징 : 하나 또는 혼합 분자 시스템, 입자들의 집합을 통해 입자 간의 상호작용을 측정한다. 두 입자를 통해 위치와 에너지 정보를 측정할 수 있고 그중 하나는 시뮬레이션을 통한 전체 분자의 시스템을 분석하는 것에 사용된다. 하나 또는 그 이상의 분자를 포함하는 원자 및 분자를 포함하여 시뮬레이션이 가능하며 여러 시간 척도에 따라 연관된 분자들 또는 원자들을 시스템에 적용해 분석할 수 있다.
- 특허전략
◇ 대중성 있는 파이썬에 시뮬레이션 코드를 구현함으로써 시장성 확보
◇ 코드 최적화를 통해 CPU time을 감소시켜 사용자의 작업속도를 향상할 수 있어 경쟁력 확보
◇ 여러 기능을 탑재하여 가격이 비싼 타사 프로그램에 비해 한정된 기능을 제공하지만, 상대적으로 접근성이 높고 가격이 저렴한 프로그램의 개발
개발과제의 기대효과
기술적 기대효과
◇ Monte carlo canonical ensemble을 이용해 내부에너지, 압력 같은 물성을 통계 열역학 관점에서 도출할 수 있다.
◇ 기존 프로그램들의 경우 포트란을 사용하기 때문에, 수정하려면 특수한 운영체제(리눅스 등)가 필요하다. 하지만 본 프로그램의 경우 대중성 있는 컴파일러인 파이썬을 이용해 소스코드를 열어둠으로써 사용자가 쉽게 접근할 수 있어 원하는 대로 일부 수정할 수 있다.
◇ 현재 제작하는 코드의 틀은 파이썬으로, 라이브러리가 다양하여 여러 기능을 사용할 수 있어 알아내고자 하는 결과 값에 따라 시뮬레이션 기능을 추가하여 성능을 향상시킬 수 있다.
◇ 개발된 기술을 활용해 알고리즘을 적용한 프로그램을 통계열역학과 접목하여 적용 범위를 확대하고 기술 활용 능력을 발전시킨다.
경제적, 사회적 기대 및 파급효과
◇ 프로그램을 구매한 학생들에게 코드를 제공해 코드를 분석할 기회를 제공한다. 또한 상대적으로 코딩 지식이 부족한 학생들은 프로그래밍을 익히고 코드의 실행 원리를 파악해 통계 열역학적 사고를 이해하고 해석하는 도구로 활용할 수 있다. 특히 코딩 관련 강의가 적은 학생들의 경우, 실험 수업 등에 활용하며 학습 효과를 높일 수 있다.
◇ 이용자들이 쉽게 접근할 수 있는 보다 값싼 프로그램을 제작하여 분자 시뮬레이션 프로그램 활용의 진입장벽을 낮출 수 있다. 특히 고가의 분자 시뮬레이션 프로그램을 구매하기 어려운 많은 학생이 프로그램을 이용하여 통계 열역학적 분석 및 코딩에 대한 학습을 통해 통계적 지식을 함양하여 잠재적인 이익을 극대화할 수 있다.
기술개발 일정 및 추진체계
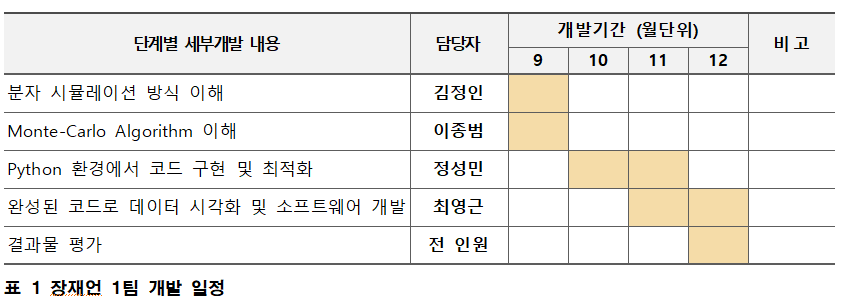
개발 일정
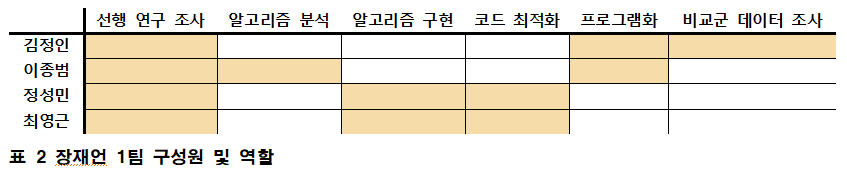
구성원 및 추진체계
설계
개념설계안
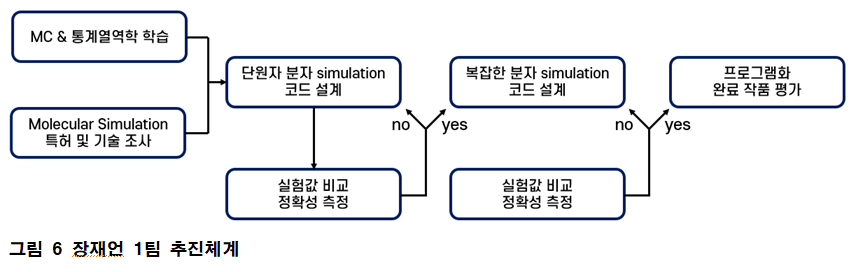
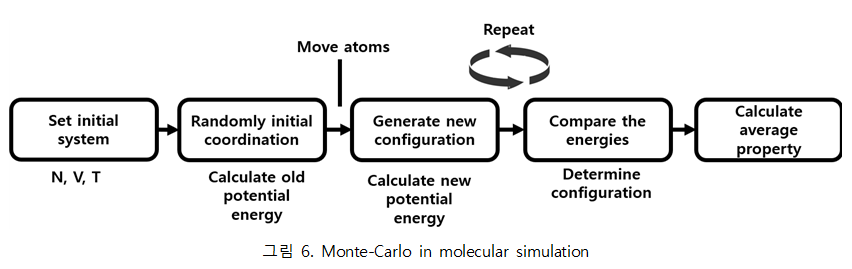
◇ Monte-Carlo in molecular simulation
분자 시뮬레이션에 몬테카를로 방법을 적용하는 것을 간략하게 나타내면 그림 6과 같다.
이론적 계산 및 시뮬레이션 상세 설계
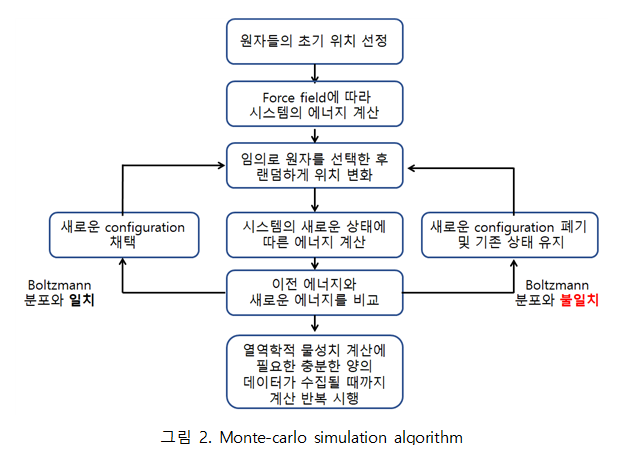
먼저 canonical ensemble 시스템에서 원자의 수, 부피, 온도를 정하여 initial system을 설정한다. 원자의 수와 시스템의 부피가 결정됐으므로 각 원자를 시스템 내부에 존재하도록 좌표를 무작위로 할당한다. 이 때 overlap을 피하기 위해 추가적인 작업이 필요하다. 처음에 결정된 configuration에서 시스템 내에 존재하는 원자를 움직이게 하여 새로운 configuration을 결정한다. 이 때 기존 configuration에서 계산한 포텐셜 에너지와 새로운 configuration에서 계산한 포텐셜 에너지를 볼츠만 분포 식을 통해 비교하여 configuration을 결정한다. 볼츠만 분포의 식은 다음과 같다.
이를 코드로 구현한 것이 그림 7과 같다.
0부터 1까지 난수를 발생시키는 라이브러리를 사용하여 기준이 되는 확률을 무작위로 도출하고 이를 포텐셜 에너지 차이를 통한 볼츠만 분포 식에 적용한다. 이를 통해 새로운 configuration이 기존 configuration보다 포텐셜 에너지가 낮은 경우 새로운 configuration을 accept하고 큰 경우는 확률적으로 accept하는 것이다. 위의 과정을 매우 많이 반복하여 평균값을 얻을 수 있는 많은 configuration 표본을 구하여 최종적으로 해당 시스템의 열역학적 물성을 도출할 수 있다. ◇ Force Field 몬테카를로를 이용하여 분자 시뮬레이션을 하기 위해서 포텐셜 에너지를 비교하는 과정이 필요하다. 다양한 특징을 갖는 분자에 대해 포텐셜 에너지를 구하는 식은 다음과 같다.
첫 번째 항은 분자 내 원자가 이루고 있는 bond에 대한 포텐셜 에너지, 두 번째 항은 분자 내 3개 원자가 이루고 있는 각도에 의한 포텐셜 에너지, 세 번째 항은 분자 내 4개 원자에 의해 생기는 torsion에 의한 포텐셜 에너지, 마지막 항은 분자 내 원자의 극성차이로 생기는 partial charge, 그리고 원자 간 거리에 의해 생기는 repulsion, attraction과 같은 interaction으로 생기는 포텐셜 에너지를 의미한다. 본 연구에서는 Argon, Methane, Ethane의 열역학적 물성을 도출하기 위해 위의 포텐셜 에너지를 구하는 식에서 Argon은 단원자 분자이기 때문에 네 번째 항의 interaction에 의한 Lennard-Jones 포텐셜 에너지만을 계산하고 Methane, Ethane은 각각 C-H bond, Ethane의 경우 C-C bond까지 존재하기 때문에 첫 번째의 bond에 의한 포텐셜 에너지를 추가하여 계산한다.
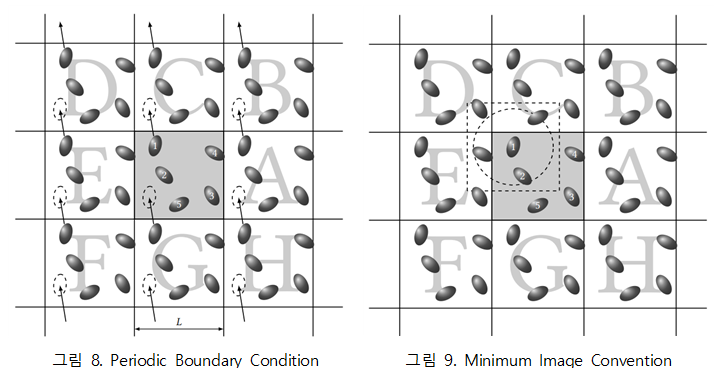
◇ Periodic Boundary Condition 코드를 통한 가상 실험을 위해 적용하는 가정이 Periodic Boundary Condition(PBC) 조건이다. PBC는 Canonical 조건에 따라 박스를 만들어내고 주변에 가상의 복제된 박스들을 구현하는 방법이다. 이로써 박스 내부에 있는 원자의 수를 일정하게 유지시킬 수 있으며 Minimum Image Convention 방법을 통해 비교적 빠르게 해당 시스템의 포텐셜 에너지를 계산할 수 있다. Minimum Image Convention은 해당 원자 주위에 가상의 박스를 만들어 해당 박스 내부에 존재하는 원자들의 포텐셜 에너지만 계산하는 방법으로 그 원자에 가까운 거리에 존재하는 원자들에 대한 포텐셜 에너지를 계산하는 것이다. 이를 통해 시스템에 주어진 원자의 수에 따라 지수함수로 증가하는 계산 량을 줄이는 것의 효과를 볼 수 있다. 이와 같은 방법을 적용할 수 있는 이유는 cutoff distance 이상의 거리의 원자들 간 포텐셜 에너지는 거의 0에 수렴하기 때문이다. 이를 코드로 구현한 것이 그림 10과 같다.
◇ Long Range Correction 앞서 포텐셜 에너지를 계산할 때 계산량을 줄이기 위해 Minimum Image Convention의 방법을 적용했다. Cutoff distance 이상의 포텐셜 에너지와 비리얼 계산은 무시되었으므로 해당하는 포텐셜 에너지를 보상하기 위해 Long Range Correction 방법을 적용한다.
위 식을 적용하여 cutoff distance 이상의 압력, 포텐셜 에너지를 보상하면 완전한 열역학적 물성을 구할 수 있다.
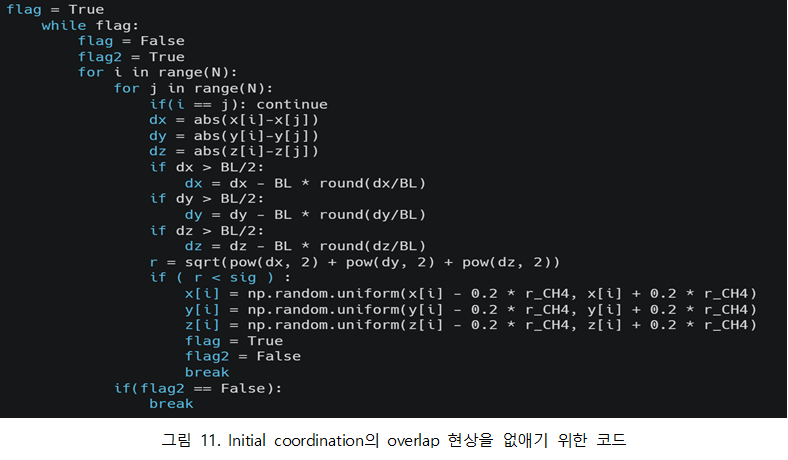
◇ Initial coordination 컴퓨터는 가상의 실험 환경이므로 현실적인 물리적 한계를 무시한다. 가상의 시스템을 구현하기 위해 무작위하게 원자의 처음 좌표를 할당하는 과정이 필수적이다. 이 때 무작위로 좌표가 할당되기 때문에 가상 시스템 내부에 존재하는 분자끼리 overlap이 되는 현상이 나타날 수 있는 것이다. 실제로 물리적으로 나타날 수 없는 현상이 가상의 시스템에서 구현된 것이다. 거리에 따른 Lennard-Jones potential energy을 보면 원자간 거리가 되게 작을 때 repulsion으로 인한 양수의 포텐셜 에너지가 기하급수적으로 증가한다. 따라서 실제로 발생할 수 없는 overlap 현상이 코드 내 가상적 공간에 구현이 되어 알고리즘에 반영되어 정확한 시스템의 포텐셜 에너지를 계산할 수 없게 된다. 그림 11은 Methane의 열역학적 물성을 구하는 시스템에서 initial coordination을 구현 후 overlap을 없애기 위한 추가적인 코드다. 실제로 계산하는 영역은 Minimum Image Convention에 의하여 한 원자의 cutoff distance에 따른 영역이다. 따라서 해당 영역에서 overlap이 생기는 것을 판별한 후 Methane의 diameter에 비례한 값을 통해 overlap된 원자가 해당 위치에서 조금씩 움직이게 하여 overlap 현상을 없애는 것이다.
◇ High density case 밀도가 높은 시스템은 분자의 수가 많거나 박스의 부피가 작아질 때를 의미한다. 이러한 시스템을 바로 구현시켜 분자 시뮬레이션을 진행하면 정확한 열역학적 물성을 구할 수 없다. 시스템이 보다 불안정한 상태에서 시작하여 평형을 이루지 못하기 때문이다. 따라서 높은 밀도를 가진 시스템은 안정화 시켜 평형이 이룰 수 있도록 천천히 박스의 크기를 줄여나가며 좌표를 안정화시키는 작업이 필수적이다.
그림 12가 높은 밀도를 가진 시스템에 대해서 좌표를 안정화시키기 위한 코드다. 밀도가 낮은 시스템으로부터 시뮬레이션을 진행하여 안정화를 시키는 함수를 통해 좌표 값을 반환시키고 위의 과정을 반복하여 최종적으로 구현하고자 하는 밀도가 높은 시스템의 initial coordination의 data로 도출될 수 있다.
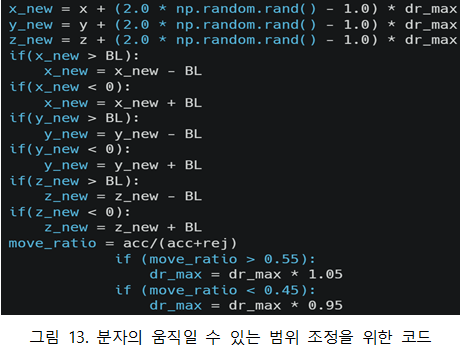
◇ Accept/reject ratio 기존 configuration를 구성하는 원자의 움직임을 통해 새로운 configuration이 만들어진 후 기존과 새로운 configuration의 포텐셜 에너지 비교를 통해 새로운 configuration을 accept 또는 reject이 되는 지 결정이 된다. Accept이 되면 새로운 configuration이 열역학적 물성을 구하기 위한 평균값에 포함되어 계산이 된다. 이 때 accept과 reject가 되는 비율을 조정해야 정확한 열역학적 물성을 구할 수 있다. 몬테카를로 방법에서 열역학적 물성을 구하는 것은 안정화된 평형인 상태에서 여러 configuration의 평균값으로부터 계산된다. Accept이 상대적으로 reject보다 너무 많은 경우는 원자의 움직임이 매우 적은 경우다. 이 때 평형상태의 여러 configuration을 고려한 것이 아닌 해당 상태와 비슷한 configuration만을 고려한 경우이기 때문에 정확하지 못한 평균값이 도출될 수 있다. 반대로 reject이 상대적으로 accept보다 너무 많은 경우는 원자의 움직임이 매우 큰 경우다. 위 경우는 reject가 너무 많아 평균값에 포함되는 configuration의 표본 개수가 적어지게 되므로 해당 시스템의 정확한 평균값을 구하지 못한 것이 된다. 따라서 원자가 움직일 수 있는 범위를 accept/reject ratio에 따라 조정하는 작업이 필수적이다.
그림 13은 accept/reject ratio에 따라 새로운 configuration을 위한 원자가 움직일 수 있는 범위를 조정시키는 코드다. accept/reject ratio가 0.45보다 작은 경우 accept를 늘리기 위해 원자가 움직이는 범위를 줄이고 accept/reject ratio가 0.55보다 큰 경우는 reject을 늘리기 위해 원자가 움직이는 범위를 늘리는 것이다.
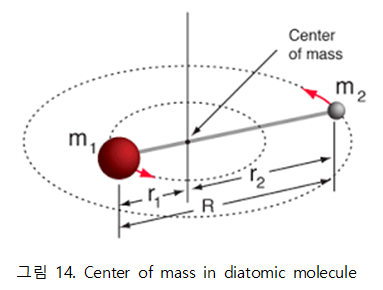
◇ Center of mass Monatomic에서 diatomic 이상으로 분자를 확장할 경우 분자의 translation을 고려하는 다른 방법이 필요하다. Diatomic의 경우 분자 내에서의 bond는 고정된 값을 지니기 때문에 기존의 방식을 사용할 경우 분자 내 bond의 일정한 거리를 유지시킬 수 없다. 예를 들어 high density case의 경우 천천히 박스의 크기를 줄여나가면서 좌표를 줄이는데, 그 과정에서 고정된 bond의 길이 또한 함께 줄어들게 되므로 적절하지 못하다. Center of mass는 분자 전체의 질량의 중심이 되는 지점으로, center of mass를 이동시킨 뒤 이를 중심으로 각각의 분자를 재배치시키는 과정을 통해 분자 내 bond의 거리를 일정하게 유지시킬 수 있다. 이 경우 구면좌표계에서의 theta, gamma값을 랜덤으로 조절하여 rotation 기능 또한 추가적으로 구현할 수 있다.
결과 및 평가
완료 작품의 소개
시뮬레이션 결과
◇ NVT ensemble에서 Internal energy (비이상에너지) 값 도출
- Argon vapor
- Methane vapor
그림 15, 16은 canonical ensemble 시스템에서 simulation을 통해 구한 열역학적 물성인 internal energy를 온도에 따라 나타낸 그래프다. Simulation을 통해 구한 비이상 internal energy를 직접적으로 NIST 실험값과 비교할 수 없다. 따라서 NIST에 기입되어 있는 Heat capacity(Cv)를 통해 간접적으로 비교할 계획이다. 이 때 통계열역학으로 구한 이상에너지에 대한 값도 필요하다. 이상에너지에 대해 구하는 방법은 차후에 다루도록 하겠다.
◇ NVT ensemble에서 Pressure 값 도출 ( P-density graph ) Density 변화에 따른 Pressure를 각 물질에 따라 시뮬레이션 한 그래프. Isothermal system으로 설정하였으며, 실선은 NIST의 reference 값을 뜻하고 세모는 시뮬레이션 결과를 뜻한다. 즉, 선에서 벗어나지 않을수록 시뮬레이션 결과가 정확함을 뜻한다.
- Argon vapor, supercritical phase
- Methane vapor, supercritical phase
- Ethane vapor, supercritical phase
◇ 기존의 다양한 상태방정식과 Simulation의 정확도 비교
- Comparison with Equation of State and simulation
그림 23, 24는 Simulation이 기존 상태방정식보다 정확하게 예측하는지 비교하기 위한 그래프다. 각각 Argon과 Methane의 P vs density graph에서 검은색 선은 NIST 실험값이고 빨간색 삼각형은 simulation으로 구한 압력 값이며 나머지 색의 삼각형들은 기존 상태방정식에서 도출된 값을 뜻한다. 그래프를 통해 Argon, Methane 둘 다 상태방정식과 simulation이 밀도가 작은 영역에서는 NIST 값과 일치하는 경향성을 보였으나 밀도가 큰 구간에서 서서히 오차가 생기는 경향성이 보이는 것을 알 수 있다. 그 중 Van der Waals 상태방정식이 가장 부정확하게 압력 값을 예측하고 있고 그 다음은 Peng-Robinson 상태방정식이 NIST값과 큰 오차를 보이고 있다. 반면 Redlich-Kwong 상태방정식은 NIST값과 근사한 경향성을 보였으나 simulation보다 상대적으로 부정확한 값을 나타냄을 알 수 있다. 따라서 밀도가 큰 구간은 본 연구로 구현한 simulation이 타 상태방정식보다 정확하게 열역학적인 물성을 예측하고 있다는 것을 알 수 있다.
◇ 시뮬레이션으로 계산한 Internal energy에 통계열역학적 이상에너지를 더하고 dU = CvdT 식을 이용해 각 물질의 Cv를 도출 위의 internal energy에 더해주는 통계열역학적 이상에너지 식은 단원자 분자인 Argon은 . 그 외의 methane이나 ethane의 경우 polyatomic ideal gas이므로 다음과 같은 식으로 계산한다.
계산된 전체 에너지를 T에 대해 플랏한 후, 각 온도에서의 기울기를 통해 Cv값을 도출해낼 수 있다.
- Argon vapor, supercritical phase
- Methane vapor, supercritical phase
- Ethane vapor, supercritical phase
정확도 분석 및 오차 경향성을 보기 위한 상대오차 그래프
그림 31를 보면 density가 300kg/m3으로 커질수록 상대오차가 크게 나옴을 알 수 있었다. 또한 그림 32에서 온도가 625K으로 커질수록 상대오차가 작게 나옴을 알 수 있었다. 즉, 상대오차는 시스템의 온도가 낮고 밀도가 커질수록 증가한다는 사실을 알 수 있었다.
프로토타입 사진 혹은 작동 장면
내용
포스터
내용
완료작품의 평가
내용
향후계획
내용