2팀
프로젝트 개요
기술개발 과제
국문 : 최적화 모델링 언어를 사용한 DWC의 simulation과 최적화
영문 : Simulation and Optimization of Dividing Wall Column using Pyomo
과제 팀명
유준재교수님1팀
지도교수
유준재 교수님
개발기간
2024년 3월 ~ 2024년 6월 (총 4개월)
구성원 소개
서울시립대학교 공과대학 화학공학과 20203400** 장**(팀장)
서울시립대학교 공과대학 화학공학과 20203400** 노**
서울시립대학교 공과대학 화학공학과 20183400** 진**
서론
개발 과제의 개요
개발 과제 요약
◇ Distillation은 전세계 에너지량의 10-15%를 차지하는 주된 에너지 사용원이며 다양한 산업의 기반이 되는 물질들을 합성하므로 Distillation 과정에서 에너지 효율성을 극대화하는 것이 매우 중요하다. 이 때 Dividing Wall Column (이하 DWC)는 에너지 효율성을 극대화한 Petyluk 구조에서 Capital cost 까지 낮춘 고효율의 Distillation 방법으로 제시되었다. 해당 구조는 Reboiler와 Condenser를 한 쌍만 사용하여 thermocouples를 이루는 Petyluk 구조에서 더 나아가 prefractionator를 main column 안으로 삽입하면서 Capital cost 까지 낮추었다.
◇ DWC는 이미 그 구조 및 다양한 디자인이 제시되었으나 공정을 모델링할 수 있는 소프트웨어의 발전이 많이 이루어지지 않아 상용화에 어려움을 겪고 있다고 한다.
◇ 따라서 Pyothon의 패키지인 Pyomo를 이용해 DWC 내부를 세부적으로 모델링하여 DWC Distillation을 시뮬레이션해보면서 DWC Distillation이 열역학적으로 우수한 구조임을 수치적으로 증명한다. 또한 해당 모델을 사용해 시뮬레이션을 및 최적화를 진행해보면서 DWC의 상용화에 도움을 주는 것을 목표로 한다.
개발 과제의 배경
◇ 에너지 효율성을 증대하고 지속 가능한 발전을 이루기 위한 다양한 Distillation 방법이 다양하게 제시되고 있으나, 기존의 Distillation 방법보다 지속 가능하며 안정적인 intensified precess 중 Dividing Wall Column(이하 DWC)는 Petyluk 구조를 전신으로 하여 열역학적 효율을 극대화하는 구조다. Petyluk 구조는 기존의 seperated columns의 한계점을 극복하고 두 가지 column의 Condenser와 Reboiler를 한 쌍으로 통합하는 thermocouples을 가능하게 했다. 이를 발전시킨 형태인 DWC는 Petyluk의 prefractionator를 하나의 column에 통합한 구조이다.
◇ DWC는 전통적인 column sequences와 비교했을 때, 에너지 사용량을 30% 이상 줄일 수 있을 것으로 예상된다. 또한 한 개의 column만으로도 운용할 수 있기 때문에 Capital cost가 매우 낮아졌으며, 물질의 purity 또한 기존의 기술들보다 높일 수 있다고 밝혀졌다.
◇ 하지만 기존의 Distillation software인 Aspen Plus 및 ChemCAD 등에는 DWC를 시뮬레이션 및 최적화할 수 있는 모듈이 존재하지 않는 상태다. 따라서 parallel column을 포함한 Chem LITE tool을 개발하는 등 다양한 연구가 이루어지고 있으나, 아직까지 공정 설계자들은 기존의 column들을 조합해서 DWC와 유사하게 시뮬레이션할 뿐이다. 이런 점은 DWC가 더 널리 상용화되는 것의 한계점이다.
◇ 따라서 DWC를 모델링하고 시뮬레이션하며 최적화를 진행하는 것은 지금의 상황에 큰 도움을 제공하여 에너지 효율이 좋은 DWC를 널리 사용하는 것에 이바지할 수 있으리라고 예상한다.
개발 과제의 목표 및 내용
◇ 연구의 목표는 기존에 개발되지 않은 DWC module을 Pyomo 패키지를 사용하여 모델링하고 시뮬레이션 및 최적화를 진행하여 상용화 가능한 DWC 모델을 제안하는 것이다.
◇ Distillation의 최신 연구 동향에 대해 조사하고 관련 기술 및 특허들이 어떻게 상용되고 있는지 알아본다. 그중 DWC 관련 시뮬레이션을 어떻게 진행하고 있는지 조사하고 관련 논문을 읽는다.
◇ Python 언어를 기반으로 한 최적화 전문 패키지인 Pyomo를 사용해서 DWC를 모델링한다. 처음에는 가장 적은 수의 단(총 5개)으로 이루어진 간단한 구조를 모델링하며, 이상적인 상황을 가정한다. 그리고 이를 발전시켜 더 많은 단을 시뮬레이션할 수 있도록 한다.
◇ 최종적으로 모델이 시뮬레이션 가능한 수준으로 제작된 이후에는 다양한 물질 및 조건(온도 및 압력 등)에 따라 최적화를 진행한다. 이 과정에서 모델을 수정하는 과정도 거친다. 이런 모델 및 시뮬레이션 결과를 제안하는 것으로, 결과적으로 에너지 효율 증대에 크게 기여할 것으로 보이는 DWC의 상용화에 기여하고자 한다.
관련 기술의 현황
관련 기술의 현황 및 분석(State of art)
- 전 세계적인 기술현황
- ◇ 증류는 화학 공정 산업에서 널리 사용되지만, 자본과 에너지를 많이 소모하는 공정으로 알려져 있다. 실제로, 화학 및 석유 정제 산업에서의 증류 작업만으로도 총 분리 에너지의 거의 53%를 차지한다고 보고되고 있다. 이러한 이유로, DWC는 에너지를 절약할 수 있는 잠재력으로 인해 학술 및 특허 문헌에서 점점 더 많은 관심을 끌고 있다. DWC는 일반적인 증류 column과 비교했을 때 최대 30%의 에너지를 절약할 수 있다고 보고되며, 또한 하나의 shell에 설치되어 일반적으로 자본 비용의 상당 부분을 절약할 수 있다.
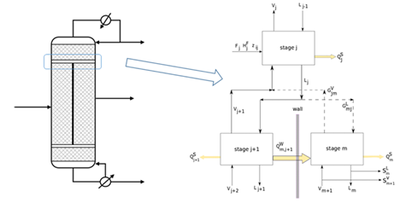
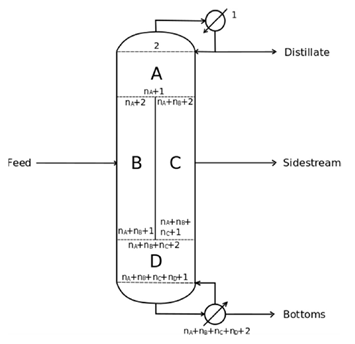
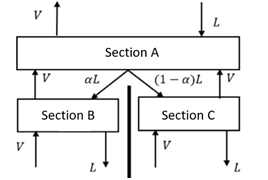
- ◇ 최근 연구에서는 DWC 모델링에 각 단계에서 기체와 액체가 평형 상태에 있다고 가정한 parallel column model을 사용해 MESH 방정식을 적용한다. 이때 MESH 방정식은 각 단계에서 들어오고 나가는 물질의 몰 흐름율이 균형을 이루는 Mass balance, 기체와 액체 사이의 평형 관계로 Equilibrium balance, 모든 성분의 몰 분율 합이 각 단계에서 1이 되도록 Summation balance, 들어오고 나가는 열량의 계산으로 Heat balance를 작성하는 것을 의미한다. 각 단계에서 들어오고 나가는 물질과 열의 양이 균형을 이루는 것을 계산함으로써 물질의 흐름과 온도를 예측하고, 분리 벽 상단과 하단에서 흐름이 어떻게 분리되는지 그 비율을 ,로 표현한다.(Fig.1) 이러한 방법론의 적용을 통해 분리 공정의 에너지 소비를 줄이고 공정 비용을 최적화하는 데 기여할 수 있다. DWC 모델링에 대한 simulation 기술의 개발을 통해 화학 공정 산업의 지속 가능성과 효율성 증진을 기대하고 있다.
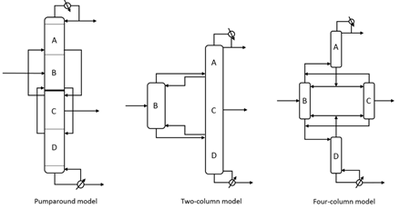
- ◇ Aspen Plus와 ChemCAD를 포함한 상용 소프트웨어 패키지에는 직접 설계 및 simulation에 사용할 수 있는 표준 DWC 모듈이 없다. 따라서 아직까지는 DWC를 simulation 하기 위해 전통적인 column을 병렬 및 직렬로 배치하는 등의 복잡하고 정확도도 떨어지는 방법을 사용해야 한다고 알려져 있다. (Fig.2).
- ◇ 최근 연구에 따르면, 방정식 기반 모델링이 DWC 시스템을 더 효과적으로 설명할 수 있다는 제안이 있다. 그러나 현재로서는 상용 소프트웨어를 이용한 DWC 모델링은 여전히 어려운 문제로 남아 있다. 이러한 도전에 대응하기 위해 Pyomo 언어가 주목받고 있는데, Pyomo는 파이썬 기반의 오픈 소스 최적화 모델링 언어로, 복잡한 프로세스 및 시스템을 수학적으로 모델링하고 최적화할 수 있다. Pyomo를 활용하면 방정식 기반 모델을 쉽게 구현할 수 있으며 DWC simulation에 활용할 수 있다. 더불어, Pyomo를 활용한 이러한 모델은 다양한 최적화 알고리즘을 적용하여 최적의 운전 조건을 탐색할 수 있다. 이러한 방식으로 Pyomo를 활용하여 DWC의 simulation과 최적화에 관한 연구를 진행함으로써, 산업 프로세스의 효율성과 경제성을 향상하는 데 중요한 역할을 할 것으로 기대된다.
- 특허조사 및 특허 전략 분석
- ◇ 분리벽형 증류탑 및 이를 이용한 네오펜틸글리콜의 정제 방법
- 출원일: 14.09.26 출원번호: 10-2014-0129368 출원인: 한화케미칼 주식회사
- 본 발명은 분리벽형 증류탑 및 이를 이용한 네오펜틸글리콜의 정제 방법에 관한 것이다. 보다 구체적으로는 네오펜틸글리콜을 포함하는 조 생성물을 고순도로 정제할 수 있는 분리벽형 증류탑 및 이를 이용한 네오펜틸글리콜의 정제 및 에너지 소비량도 종래에 비하여 절감하는 방법이 제시되어 있다.
- 해당 방법은 고순도의 결과물을 얻기 위해 DWC를 사용하고 있는데, 이를 통해 Dividing Wall Column이 높은 순도를 얻기 위한 좋은 방법으로서 다양하게 개발되고 있음을 알 수 있다.
- ◇ 듀얼 모드 분리벽형 증류탑
- 출원일: 12.09.19 출원번호: 10-2012-0103959 출원인: 주식회사 엘지화학
- 본 발명은 분리벽형 모드 및 단일벽형 모드 간의 상호 전환이 가능한 듀얼 모드 분리벽형 증류탑 및 상기 듀얼 모드 분리벽형 증류탑을 이용한 증류방법에 관한 것이다. 기존의 단일벽형 모드 증류탑에 비해 장치비용 및 에너지를 절약할 수 있으며, 생산성을 향상할 수 있다. 또한, 공정 셧다운 없이 분리벽형 모드 및 단일벽형 모드 간의 상호 전환이 가능하여, 장치의 이상으로 셧다운 시 발생할 수 경제적 손실을 방지할 수 있다.
- 해당 기술은 자본 비용 및 운영비용을 낮추는 것에 초점을 두는데, 이를 통해 Dividing wall column의 효율적인 상용화를 위해 다양한 기술이 개발되고 있음을 알 수 있다.
개발과제의 기대효과
기술적 기대효과
- ◇ DWC Distillation 성능의 정확한 모델링 및 simulation: Pyomo를 활용하여 DWC의 성능을 정확하게 모델링하고 시뮬레이션함으로써, DWC Distillation의 열역학적 우수성을 수치로 입증할 수 있다. 이를 통해 실제 공정에서 DWC의 성능을 더 잘 이해하고 평가할 수 있게 될 것이다.
- ◇ 분리 공정의 운영비용 감소 및 효율성 향상: 공정의 동적인 운영 조건을 실시간으로 모니터링하고 조정할 수 있다. 이는 예상치 못한 운영 조건 변화에 신속하게 대응할 수 있게 해주며, 이로 인한 생산성 손실을 최소화하여 용을 절감할 수 있다. 분리해야 하는 성분 간의 상호작용과 column 내부의 물질 전달 효율을 정확하게 분석하고 온도, 압력, Feed 위치 등 최적화를 통해 효율적인 공정을 운영할 수 있다.
경제적, 사회적 기대 및 파급효과
- ◇ 산업 경제성 강화: DWC Distillation 기술의 개발을 통해 증류 공정의 에너지 소비를 줄이고 공정 비용을 최적화할 수 있다. 이는 화학 및 석유 정제 산업과 같은 산업 분야에서 자본과 에너지를 효율적으로 활용할 수 있도록 도와준다. 특히, DWC의 에너지 효율성을 최적화하는 기술은 비용을 절감하고 이익을 극대화하는 것에 이바지할 것으로 기대된다.
- ◇ 지속 가능한 발전 촉진: 에너지 절약과 효율적인 자원 활용은 지속 가능한 발전을 위한 중요한 요소이다. DWC Distillation 기술의 개발은 화학 공정 산업의 지속 가능성을 높일 수 있다. 더 적은 에너지 소비로 같은 생산량을 유지할 수 있으므로 화학 공정의 환경 영향을 줄일 수 있다.
- ◇ 기술 혁신과 경쟁력 강화: Pyomo를 활용한 최적화 모델링과 MESH 방정식을 적용한 DWC 모델링은 산업적인 기술 혁신을 촉진한다. 이러한 기술적 발전은 기업들의 경쟁력을 향상하고 산업 내에서의 선도적인 위치를 확보하는데 기여할 수 있다. 또한, 새로운 기술을 개발하고 상용화함으로써 산업 내에 새로운 시장을 개척할 수 있다.
기술개발 일정 및 추진체계
개발 일정
3월 : Distillation 전반에 관련한 최신 연구동향 조사
3월 : DWC 관련 특허와 설비의 최신동향과 현 시점 기술의 한계점 조사
4-5월 : Python 중 Pyomo pacakge를 사용해 모델링 및 시뮬레이션
4-5월 : 시뮬레이션 결과를 바탕으로 최적화 및 열역학적 우수성 검토, 연구
5-6월 : 최적의 모델링 방법 제시
구성원 및 추진체계
◇ 증류의 최신 동향에 관한 연구-장민주, 노지현
- 증류 기술의 최근 발전에 대한 포괄적인 문헌 검토를 통해서 현재 산업의 방향성을 파악하고, 지속가능한 발전을 위한 방안을 구상해본다.
◇ DWC(Dividing Wall Column) 특허 및 기술 동향 조사-노지현, 진형민
- 최근 DWC 설계의 운영적, 경제적, 환경적 측면을 비교하여 기술 동향과 한계를 분석한다. 이에 대응할 개선안을 구상해본다.
◇ Python에서 Pyomo를 사용한 모델링 및 시뮬레이션-장민주, 노지현
- Pyomo 패키지에 대한 숙련도를 향상시키고, 필수 변수와 방정식을 통합하여 DWC 공정의 모델 구조를 설계한다. 시뮬레이션을 수행하여 다양한 시나리오에 대한 결과를 도출한다.
◇ 시뮬레이션 결과에 따른 최적화 및 열역학적 평가-장민주, 노지현, 진형민
- 시뮬레이션 데이터를 통해 공정의 효율성과 출력에 미치는 영향을 식별한다. 최적화 알고리즘을 적용하여 최적의 작동 조건을 파악한다.
◇ 최적의 모델링 방법 제시-장민주, 노지현, 진형민
- 에너지 소비, 분리 효율성 등을 기준으로 사용하여 최적화된 모델의 열역학적 효율성을 평가한다. 최적화된 모델을 기존과 비교하여 잠재적인 개선사항을 파악해본다.
설계
목표 달성을 위한 설계 방법
연구 과정 개요
| 단계 | 목표 | 세부 목표 | 단 수 (각 A,B,C,D Section) | Cp |
|---|---|---|---|---|
| 1단계 | 가장 기본적인 DWC 설계 | Set, Parameter, Variable, Constraint, Objective 설정 | 2, 1, 1, 2 | 상수 |
| 2단계 | 현실적 형태로 정교하게 수정 | 단 수 추가, Cp 온도변화 영향 고려 | 5, 10, 10, 5 | 상수, 온도에 관한 식 |
| 단계 | 목표 | 세부 목표 | Objective |
|---|---|---|---|
| 3단계 | Parameter의 변수화 | RR, BR 변수화 (Reflux Ratio, Boil-up Ratio), F_S의 변수화 (Side stream에서 나가는 양) | Out stream에서 각 component의 양 최대화 |
| 4단계 | Cost Function 설정을 통해 현실에 부합하는 정교한 최적화 | Operation Cost 고려 (최소화)
Operation Cost + Capital Cost 모두 고려 (최소화) |
alpha, beta 변수화 (Interchange에서 분리 비율)
비용을 고려한 단수 최적화 spec 상향 조정하여 비교 |
상세설계 내용
- 1단계) Pyomo(Python 기반의 최적화 언어)를 통한 기본 모델링
- ◇ Pyomo는 Python을 기반으로 하는 최적화 전용 언어다. 먼저 Set 클래스를 통해 우리가 사용하는 세 가지 component인 Benzene, Toluene, m-Xylene의 앙투안 계수 및 Cp를 포함한 물성을 적어준다. 그리고 Var(Variable) 클래스를 사용해서 우리가 진행하는 최적화 모델에 필요한 decision variable들을 정의한다. 이것에는 각 단의 온도와 압력 및 각 단에서 각 물질의 액체 및 기체 분율 등을 포함한다. 마지막으로 모델 내에서 상수로 취급할 Parameter들을 모델 밖에서 정의하는데, 이는 각 섹션에서의 단의개수 및 Feed의 조성, Reflux Ratio와 Boil-up Ratio 등을 포함한다.
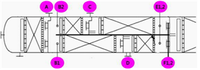
- ◇ DWC 모델은 분리벽이 있다는 점이 기존 모델과의 차별점이므로, Dividing이 발생하는 부분을 정밀하게 계산하기 위해 4가지 Section으로 나누어 코드를 진행했다. A는 Rectifying Section, B는 Left wall Section, C는 Right wall Section, D는 Stripper Section이다(Fig.5). 또한 가장 간단한 코드를 진행하기 위해서 A, B, C, D Section에 각각 2, 1, 1, 2개의 단만 있다고 가정하고 코드를 세웠다.
| 표기 | 의미 | 초깃값 | 경계 |
|---|---|---|---|
| m.T | Temperature at tray N | - | (300, 450) |
| m.L | Liquid stream from tray N | 6 mol/s | 12 mol/s |
| m.V | Vapor stream from tray N | 3 mol/s | 6 mol/s |
| m.HV | Enthalpy of vapor at tray N | - | (0, 100) |
| m.HL | Enthalpy of liquid at tray N | 30 | (0, 100) |
| m.F | Feed flow rate into each tray | 1 mol/s | (0, F_F) |
| m.x | Liquid mole fraction at tray N | 1/(m.C) | (0,1) |
| m.y | Vapor mole fraction at tray N | KJ/s | (0,1) |
| m.QC | Cooling duty at Condenser | KJ/s | (-500, 0) |
| m.QH | Heating duty at Reboiler | 0 | (0, 500) |
| m.K | Vapor-Liquid equilibrium constant | 0 | (0,20) |
| m.P_sat | Saturation pressure | 1 | (0,20) |
| 표기 | 의미 |
|---|---|
| m.C | comp = ['A','B','C'] 모든 구성요소에 대해 반복 |
| m.N | RangeSet(N_A + N_B + N_C + N_D) 모든 트레이에 대해 반복 |
| 표기 | 의미 | 초깃값 |
|---|---|---|
| N_A | Rectifying Section tray numbers | 2 |
| N_B | Left wall section의 tray numbers | 1 |
| N_C | Right wall section의 tray numbers | 1 |
| N_D | Stripper section의 tray numbers | 2 |
| F_F | Feed molar flow rate | 1 mol/s |
| x_F | Feed composition | "A": 0.3, "B": 0.4, "C": 0.3 |
| N_F | Feed tray | left wall middle tray |
| T_F | Feed temperature | 330 K |
| P | Column pressure | 1 bar |
| RR | Reflux ratio | 5 |
| BR | Boil-up ratio | 2 |
| N_S | Side stream tray | right wall middle tray |
| F_S | Side molar flow rate | 0.1 |
| alpha | Liquid spit ratio | 0.5 |
| beta | Vapor split ratio | 0.5 |
- ◇ 또한 Constraint은 최적화를 진행할 때 최적화하려는 목표가 충족해야 하는 제한 사항들을 의미하는데, Mass Balance와 Energy Balance 및 Antoine Equation, 각 단의 평형상수, 각 component의 액체 및 기체 분율 총합 제한 등을 Constraint에 적어주었다. 이렇게 함으로써 최적화를 진행할 때 화학적인 조건을 만족하는 답을 얻을 수 있다.
| 식 | 의미 |
|---|---|
| @m.Constraint(m.C, m.N) def Equilibrium(m, c, n): return m.y[c,n] - m.K[c,n] * m.x[c,n] == 0 |
• 반응물과 생성물의 농도가 평형상수에 의해 균형을 이루는 상태를 나타낸 제한조건 |
| @m.Constraint(m.N) def Implicitx(m, n): return sum(m.x[c,n] for c in m.C) == 1 |
• 액체 분율의 총합이 항상 1이 되어야 한다는 제한조건 |
| @m.Constraint(m.C, m.N) def Keq_def(m, c, n): return m.K[c,n] * P - m.P_sat[c,n] == 0 |
• 이상적인 상태에서의 화학적 평형을 설명하는 제한조건 |
| @m.Constraint(m.C, m.N) def AntoineEq(m, c, n): from math import exp return m.P_sat[c,n] == ((np.e)**(Data[c]['Ant_C1'] - Data[c]['Ant_C2']/((m.T[n]-273) + Data[c]['Ant_C3']))) / 100 |
• 주어진 온도에서 모든 성분의 증기압을 Antoine 방정식을 사용하여 계산한다는 제한조건 |
| @m.Constraint(m.N) def Refluxratio(m, n): if n == 1: return m.V[n+1] * (RR) == m.L[n] * ((RR) + 1) else: return pyo.Constraint.Skip |
• Condenser의 reflux ratio를 계산하여 설정하는 제한조건 • 나머지 단에서는 해당 제한조건이 적용되지 않음 |
| @m.Constraint(m.N) def Boilupratio(m, n): if n == N_T: return m.L[n-1] * (BR) == ((BR) + 1) * m.V[n] else: return pyo.Constraint.Skip |
• Reboiler의 boilup ratio를 계산하여 설정하는 제한조건 • 나머지 단에서는 해당 제한조건이 적용되지 않음 |
| @m.Constraint(m.N) def implicitbalance(m, n): return sum(m.x[c,n] for c in m.C) - sum(m.y[c,n] for c in m.C) == 0 |
• 기체 분율의 총합이 항상 1이 되어야 한다는 제한조건 |
| @m.Constraint() def sidestream_balance(m): return sum(m.LS[n] for n in m.N) == F_S |
• 각 단에서 side stream의 액체 molar flow의 합이 정의된 side stream의 총 molar flow와 같아야 한다는 제한조건 |
| @m.Constraint(m.N) def sidestream_distribution(m, n): if n != N_S: return m.LS[n] == 0 else: return pyo.Constraint.Skip |
• side stream 단이 아닌 경우 해당 단에서의 side molar flow를 0으로 설정한다는 제한조건 • side stream 단에서는 적용되지 않음 |
| @m.Constraint() def feedstream_balance(m): return sum(m.F[n] for n in m.N) == F_F |
• 모든 단에서의 feed stream의 총 molar flow는 F_F로 설정한 값과 같아야 한다는 제한조건 |
| @m.Constraint(m.N) def feedstream_distribution(m, n): if n != N_F: return m.F[n] == 0 else: return pyo.Constraint.Skip |
• feed 단이 아닌 각 단에서 feed stream의 molar flow는 0이어야 한다는 제한조건 • feed 단에는 적용되지 않음 |
- ◇ 이때 Mass balance 및 Energy Balance는 각 섹션마다 정의되어 있어서 코드가 매우 길다. 따라서 분리벽이 고려되어야 하는 단만 대표적으로 해당 보고서에 작성했다.
| 식 | 의미 |
|---|---|
| 분리벽을 고려한 Mass balance | @m.Constraint(m.C, m.N) def mb(m, c, n): elif n == tray_B_fst and n != tray_B_lst: return ( (m.L[n]+m.LS[n]) * m.x[c,n] + m.V[n] * m.y[c,n] - (alpha) * m.L[tray_A_lst] * m.x[c,tray_A_lst] - m.V[n+1] * m.y[c,n+1] - m.F[n] * x_F[c]) == 0 |
| 분리벽을 고려한 Energy balance | @m.Constraint(m.N) def energybalance(m, n): elif n == tray_B_fst and n!= tray_B_lst: return ( (m.L[n]+m.LS[n]) * m.HL[n] + m.V[n] * m.HV[n] - (alpha) * m.L[tray_A_lst] * m.HL[tray_A_lst] - m.V[n+1] * m.HV[n+1] - m.F[n] * H_F) == 0 |
- 2단계) 현실에 적합한 방향으로 모델 수정
- ◇ 첫 번째로, 단 수가 (2, 1, 1, 2)인 상황은 현실을 충분히 반영하지 못하므로 (5, 10, 10, 5)인 상황으로 모델의 단 수를 수정한다. 이 과정에서 ‘infeasible(실현 불가능)’이라는 오류를 수정하며 모델을 발전시켰다.
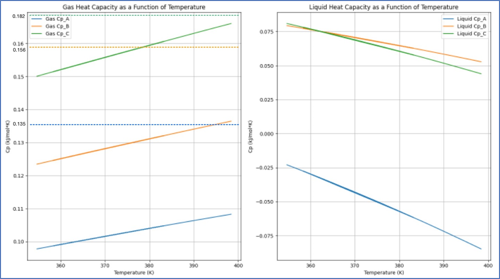
- ◇ 두 번째로, 상수로 취급했던 Cp를 온도에 대한 식으로 수정한다. 이 과정에서 Cp가 포함된 모든 식을 수정한다. 또한 온도 범위에 따른 각 component의 Cp coefficient를 새로운 딕셔너리로 입력한다.
- ◇ 원래 상수로 사용했던 Cp 값들은 gas phase일 때의 Cp값이다. Fig.6의 왼쪽 그래프에서는 Cp를 그래프로 설정하면 상수로 설정한 값들(점선으로 표시된 평형선)과 꽤 차이가 난다는 것을 알 수 있다. 또한 liquid phase(우측) 값도 크게 차이가 난다. 따라서 Cp를 온도에 따른 함수가 되도록 수정해 준 것이 모델의 정교함에 크게 기여했다고 볼 수 있다.
- 3단계) Parameter의 변수화
- ◇ 상수로 두었던 RR, BR,F_S 를 변수로 지정해 주어 모델에 맞는 최적의 값을 도출한다.
| 식 | 의미 | |
|---|---|---|
| 변경 전 | BR = 2 RR = 5 F_S = 0.39 |
• 상수로 값을 지정 |
| 변경 후 | RR_max = 30 BR_max = 30 m.BR = pyo.Var(domain=pyo.NonNegativeReals, bounds=(0.1, BR_max), initialize=2) m.RR = pyo.Var(domain=pyo.NonNegativeReals, bounds=(0.1, RR_max), initialize=5) m.FS = pyo.Var(domain=pyo.NonNegativeReals, bounds=(0, F_F), initialize = F_S) |
• RR_max(reflux ratio의 상한)과 BR_max(boilup ratio의 상한)를 지정 • 지정된 범위 (0.1~max) 안의 변수로 RR, BR을 설정 • 지정된 범위 (0.1~F_F) 안의 변수로 설정 • 초깃값은 F_S값으로 설정 |
- ◇ 최적화의 목표가 되는 Objective는 가장 light한 component인 Benzene 및 가장 heavy한 component인 m-xylene의 순도를 최대화하는 것으로 설정했다.
| 식 | 의미 |
|---|---|
| @m.Objective(sense=pyo.maximize) def objective(m): return m.y["A", 1] + m.x["C", N_T] |
• 1단에서 A의 기체 농도를 최대로, 마지막 단에서는 C의 액체 농도를 최대로 하는 목표 설정 |
- 4단계) Operation 및 Capital Cost Function 고려
- ◇ 지금까지 모델을 발전시켜 오는 과정에서는 Benzene 및 m-xylene의 순도를 최대화하는 것을 목표로 삼았다. 하지만 이제부터는 Operation Cost를 최소화하는 것을 목표로 설정하여, 실질적으로 column을 운용할 때 도움이 되는 최적화 모델링을 진행하려고 한다. 마지막 단계에서는 Capital Cost까지 설정해 보았다.
- ◇ Operation Cost의 경우, Feed 물질의 가격과 전기 등의 비용을 포함하는 가격이지만, 해당 보고서에서는 Condenser와 Reboiler에서 각각 사용하는 cooling water(냉각수)와 hot steam만을 고려하기로 했다. 각각의 가격은 0.001cent/kg, 1.2cent/kg라고 설정했다. 이를 토대로 Operation Cost를 구성하는데, 냉각수는 Condenser에서만 사용하고 hot steam은 Reboiler에서만 사용한다고 가정했다. 따라서 냉각수의 단위가격과 Condenser의 사용량을 곱하고, hot steam의 단위가격과 Reboiler의 사용량을 곱하면 Operation Cost를 얻을 수 있다.
| 변경 전 | 변경 후 | |
|---|---|---|
| Constraint | 변화 없음 | @m.Constraint(m.N) def p_spec_purity(m, n): return m.y["A", 1] >= 0.99 @m.Constraint(m.N) def p_spec_recovery(m, n): return m.x["C", N_T] >= 0.95 @m.Constraint(m.N) def p_spec_side(m, n): return m.x['B', N_S] >= 0.95 • 기존에 objective였던 Benzene(A), m-xylene(C)의 spec이 constraint로 추가 • Side stream으로 분리되는 Toluene(B)의 spec도 constraint로 추가 |
| Objective | @m.Objective(sense=pyo.maximize) def objective(m): return m.y["A", 1] + m.x["C", N_T] |
@m.Objective(sense=pyo.minimize) def cost(m): return -C_QC * m.QC + C_QH * m.QH • C_QC는 냉각수, C_QH는 스팀의 단위 가격 • m.QC(Condenser의 heat duty)는 음수이므로 – 붙임 |
- ◇ 첫 번째로(Model 1), alpha와 beta를 변수화한다.
- ◇ 두 번째로(Model 2), 단 수를 한 단씩 늘려가며 최적을 확인한다. 이때 어떤 섹션이 가장 단 수 증가에 큰 효율을 내는지 확인하기 위해서 섹션마다 진행한다. A, D 섹션은 5개에서 시작해서 15개까지 단을 늘리고, B와 C섹션은 단 수가 같아야 하므로 각 10개에서 20개까지 늘린다. 그리고 그래프를 확인하여 최적 단을 찾는 것을 목표로 한다. (* 나머지 섹션은 고정 단수 상태에서 하나의 섹션만 단수 최적화 진행)
- ◇ 마지막으로(Model 3), 지금까지는 Operation Cost를 최소화하는 것만을 목표로 잡아 왔으나, 이제는 Capital Cost까지 포함하여 가장 최적의 단 수를 찾으려고 한다.
- ◇ Capital Cost는 자본 비용으로써 미래의 이득 및 이윤 창출을 위해 투자되는 비용을 의미한다. Capital Cost에는 많은 항목이 포함되지만, 해당 보고서에서는 tray를 설치하는 비용만을 Capital Cost로 보려고 한다. 한 단을 설치할 때 필요한 cost는 이라고 설정할 수 있다. 이때 Capital Cost는 일차함수 형태라고 가정한다.
- ◇ 이 때 Capital Cost는 year단위로 설정되기 때문에, Capital Cost를 추가하기 전에, 기존의 Operation Cost의 단위를 수정하는 과정이 필요하다. 원래 Opaeration Cost 단위를 다음과 같이 수정해 주었다.
- 𝑐𝑒𝑛𝑡/𝑘𝑔×𝑘𝐽/𝑠𝑒𝑐×1𝑘𝑔/2000𝑘𝐽×1$/100𝑐𝑒𝑛𝑡×3600𝑠𝑒𝑐/(1 ℎ𝑜𝑢𝑟)×24ℎ𝑜𝑢𝑟/1𝑑𝑎𝑦×(365 𝑑𝑎𝑦)/(1 𝑦𝑒𝑎𝑟)=[𝑪_𝑸𝑯∙𝑸𝑯+𝑪_𝑸𝑪∙𝑸𝑪]×𝟏𝟓𝟕.𝟔𝟖 $/𝐲𝐞𝐚𝐫
- 이때 Stripping 단에서 사용되는 hot steam은 vaporization energy만 사용된다고 가정하며, 이때의 vaporization energy는 이다. 이에 따라 Operation 및 Capital Cost의 단위를 통일하여 그래프를 plot한다.
| 식 | 의미 | |
|---|---|---|
| Operation Cost | N = range(0, 10+1) obj_obj = {} obj_year=[] for n in N: m = makingcolumnmodel(5+n,10+n,10+n,5+n) solver = pyo.SolverFactory('ipopt') result = solver.solve(m, tee= True) obj_obj.setdefault(n, pyo.value(- m.QC * C_QC + m.QH * C_QH)) obj = obj_obj.values() for i in obj: obj_year.append(i * 157.68) plt.plot(N, obj_year, 'b', label='Utility cost' ) plt.grid(True) plt.legend() |
• n을 0에서 10까지의 범위로 설정 • 계산된 Operation cost를 저장할 딕셔너리와 리스트를 만들고 n에 대해 반복 (0부터 10까지) • n의 값에 따라 단 수가 바뀐 column의 결과를 모든 n에 대해 구하고 출력 • 딕셔너리의 값을 리스트로 변환 • Operation cost 리스트의 값에 대해 단위 통일 ($/tray·year로 변환) • n에 따른 Operation cost 플롯 |
| Capital Cost | y = [(4400*tray ) for tray in N] plt.plot(N, y, 'g', label = 'Capital cost') plt.grid(True) plt.legend() |
• 각 tray 수에 따른 Capital cost 계산 • Capital cost 플롯 |
결과 및 평가
개발 과제 핵심 결과
개요
| N of trays | alpha, beta | 목표 spec | 비고 | |
|---|---|---|---|---|
| Base Model | 5, 10, 10, 5 | 상수 (각 0.5) | m.y["A", 1] >= 0.99 m.x["B", N_S] >= 0.95 m.x["C", N_T] >= 0.95 |
RR, BR, F_S 변수 (각 m.RR, m.BR, m.FS) |
| Model | N of trays | alpha, beta | 목표 spec | 비고 |
|---|---|---|---|---|
| Model 1 | 5, 10, 10, 5 | 변수화 | m.y["A", 1] >= 0.99 m.x["B", N_S] >= 0.95 m.x["C", N_T] >= 0.95 |
최적값 (alpha, beta) = (0.2716, 0.3527) |
| Model 2 | A Section 5~15단 B,C Section 10~20단 D Section 5~15단 |
변수 | m.y["A", 1] >= 0.99 m.x["B", N_S] >= 0.95 m.x["C", N_T] >= 0.95 |
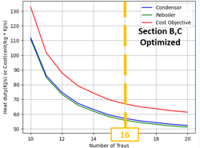
최적 단 수 (A, B&C, D) = (9, 16, 9) |
| Model 3 | 각 섹션 1단씩 추가하며 에너지 분석 | 변수 | m.y["A", 1] >= 0.99 m.x["B", N_S] >= 0.95 m.x["C", N_T] >= 0.95 m.y["A", 1] >= 0.99 m.x["B", N_S] >= 0.99 m.x["C", N_T] >= 0.99 |
현실에 가깝게 순도 목표 조정 |
◇ 먼저 Base Model은 각 섹션 당 5, 10, 10, 5개의 단 수를 가지며, alpha와 beta는 상수로 가지만 RR, BR 및 F_S는 변수로 설정된 코드이다. 이는 Table.3의 3단계를 끝낸 모델에 해당한다. 결과 분석에는 해당 Base Model을 모든 비교의 기준으로 삼을 것이다. 이때 improved model인 Model 1~3에서 RR, BR 및 F_S는 계속 변수로 설정되어 있음을 알린다.
◇ 이때 목표 스펙에서 A=Benzene, B=Toluene, C=m-Xylene을 의미함을 다시 한번 밝힌다. A는 light component로서 기체 분율(y)에서 목표 순도를 설정하고, B와 C는 상대적으로 heavy한 component로서 액체 분율(x)에서 목표 순도를 설정해 주었다.
결과
- Model 1) alpha 및 beta의 변수화
- ◇ alpha 및 beta를 상수로 두었다가 변수로 설정했을 때 최적화되는 alpha, beta값과 Operation cost profit(%)은 다음과 같다.
| 분류 | Parameters | Optimized Variable | Energy/Cost Reduction |
|---|---|---|---|
| α, β | alpha = 0.5 beta = 0.5 |
m.alpha = 0.27 m.beta = 0.35 |
- |
| QC | -183.717 kJ/s | -112.059 kJ/s | 39.01% |
| QH | 182.640 kJ/s | 110.802 kJ/s | 39.34% |
| Operation Cost | 219.351 (cent/kg)*(kJ/sec) | 133.074 (cent/kg)*(kJ/sec) | 39.33% |
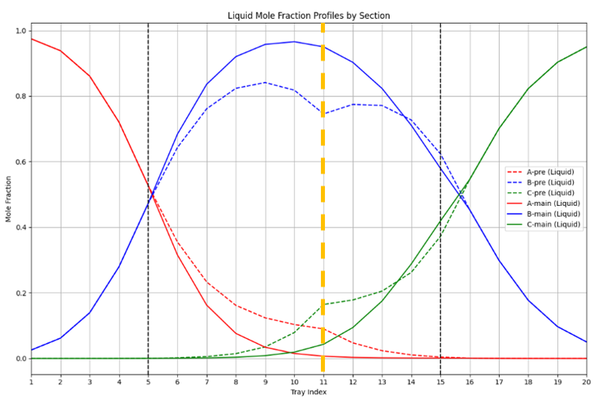
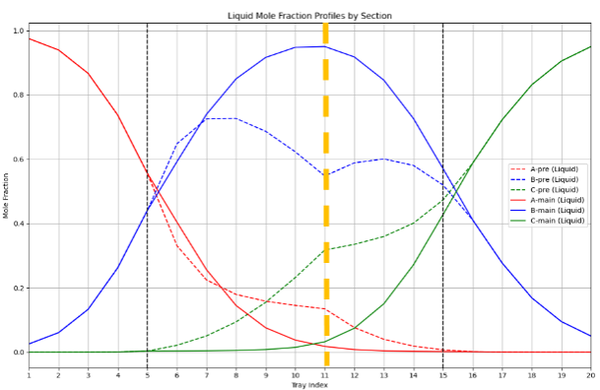
- ◇ alpha와 beta를 상수로 설정했을 때와 변수로 설정했을 때의 column 내부의 x(액체) 및 y(기체) 몰 분율 profile은 다음과 같다.
- ◇ Objective에서 40%에 가까운 효율을 얻게 된 첫 번째 이유로는, alpha, beta의 최적화를 통해 liquid와 vapor를 main column 쪽으로 더 recycle 해준다는 것을 볼 수 있다. A/B와 B/C의 분리를 이루어야 하는 main column으로 이미 어느 정도 고순도로 분리된 재순환된 기체와 액체를 보내주어 복잡한 분리 과정의 에너지 소비를 감소시킨다. 이를 통해 reboil 양과 reflux양을 줄일 수 있다. 즉 적은 에너지 소비로 prefractionator에서 A와 C의 분리를 이루면서도 main column에서 purity spec을 만족하는 solution을 찾은 결과인 것이다.
- ◇ 두 번째 이유는, 최적화 이후 side stream이 나가는 단(N=21)에서 B의 액상 농도가 최고점에 있다. Side stream은 B를 분리 해내는 것이 목표인데, 최적화 이후 N_S단에서 B의 액상 농도가 최고점에 있다. 이는 적은 에너지 소비로 높은 순도의 B를 효율적으로 분리 해낼 수 있는 것을 의미한다.
| x_F = {0.3, 0.4, 0.3} | Liquid Composition of Feed Tray |
|---|---|
| Base Model | {"A": 0.09, "B": 0.75, "C": 0.17} |
| Model 1 | {"A": 0.14, "B": 0.55, "C": 0.32} |
- ◇ 세 번째 이유는, Feed가 유입되는 단의 조성이 실제 Feed의 조성과 가까워졌기 때문이라고 볼 수 있다. 최적화 이후 prefractionator 내부의 Feed 단(N=11, 노란 점선)에서 액상과 기상의 농도가 Feed 혼합물의 농도(Benzene = 0.3, Toluene = 0.4, m-Xylene = 0.3)와 비슷하게 바뀌었다(Table.21). 이는 Feed가 투입된 tray에서 성분들이 안정적으로 분포되어, 불필요한 재혼합이 발생하지 않는다는 것을 의미한다. 따라서 분리 과정이 더 효율적으로 진행되며, 에너지 효율이 높아졌다는 것을 알 수 있다.
- Model 2) 단 수의 변화
- ◇ 단 수를 A섹션에서 5~15개로, B 및 C섹션에서 10~20개로, C섹션에서 5~15개로 각각 바꿨을 때의 Operation cost plot은 다음과 같다.
| Tray Number | Operation Cost |
|---|---|
| [ A, B, C, D ]= [ 5, 10, 10, 5 ] | 133 (cent/kg)*(kJ/sec) |
| Optimized Section | Change of Tray Number | Operation Cost (cent/kg)*(kJ/sec) | Cost Reduction |
|---|---|---|---|
| N_A | [ 9, 10, 10, 5 ] | 84 | 36.74 % |
| N_B, N_C | [ 5, 16, 16, 5 ] | 67 | 49.56 % |
| N_D | [ 5, 10, 10, 9 ] | 81 | 38.86 % |
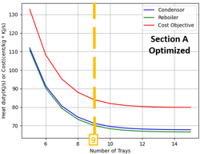
- ◇ 이를 보면 A 및 D섹션에서 단 수가 9가 되었을 때 더 이상의 단 수 증가는 무의미한 것으로 보이며, B 및 C섹션의 경우 16개 이상의 단 수 증가는 무의미한 것으로 보인다. 따라서 최적 단수는 각각 9, 16, 9개라는 것을 알 수 있었다.
- ◇ 또한 B와 C섹션에서 가장 에너지 효율의 폭이 큰 것으로 보이는데, 이는 C(Right wall)에서 Benzene과 Toluene의 분리 및 Toluene과 m-xylene을 분리하고 있으므로 단 수를 늘렸을 때 그 이득도 크게 나타나는 것으로 보인다.
- Model 3) Capital Cost를 포함한 최적화 (total cost minimize)
- ◇ spec 변경 전후에 따른 Operation Cost & Capital Cost 그래프는 다음과 같다. 이때 Operation Cost의 경우 A, B & C, D 각 섹션의 단을 한 단씩 늘려가며 계산한 값이다. 따라서 단 수는 (5, 10, 10, 5)에서 (6, 11, 11, 6)으로, (7, 12, 12, 7)으로 증가해 간다. 따라서 전체 단의 개수가 4개씩 증가하므로 Capital Cost는 4400 dollar/year로 계산할 수 있다.
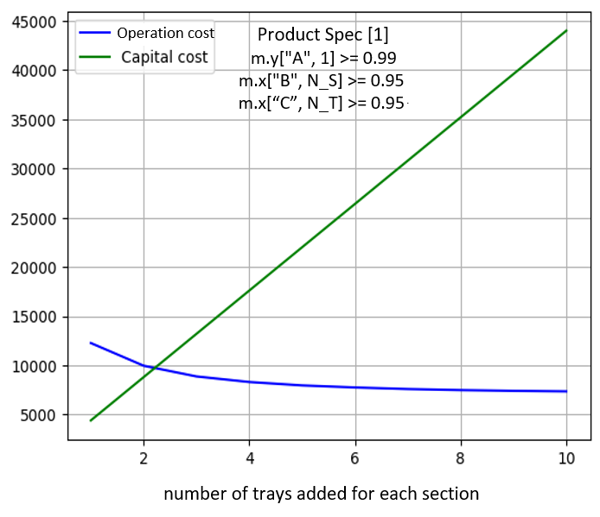
- ◇ spec을 변경하기 전의 결과를 보면(fig.13), Capital Cost의 기울기가 Operation Cost의 접선 기울기보다 항상 크다는 것을 알 수 있다. 이는 (5, 10, 10, 5)에서 더 이상 단 수를 늘릴 필요가 없음을 의미한다. 자본 비용 투자를 늘려도 에너지 이득이 크지 않기 때문이다. 이런 결과를 보고 Toluene과 m-Xylene의 spec을 0.95에서 0.99로 상향 조정하여 새로운 그래프(fig.14)를 얻었다.
| N of Tray | 2 | 3 | 4 |
|---|---|---|---|
| Slope | 21510 | 9589 | 3413 |
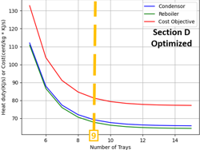
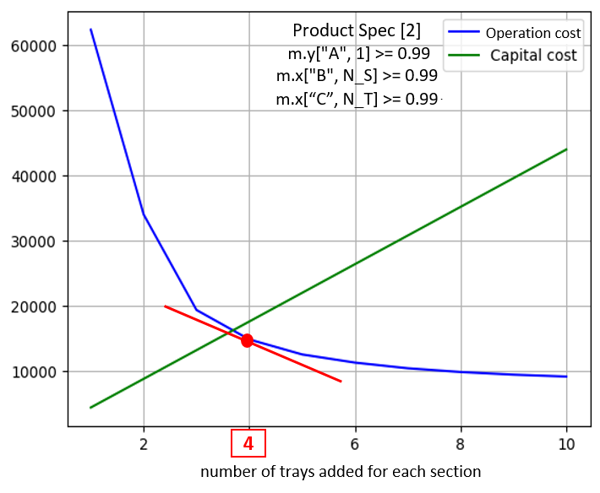
- ◇ spec을 상향 조정한 결과를 보면(fig.14), x축이 4일 때 (즉 (A, B, C, D) = (9, 14, 14, 9)일 때) 이후부터는 Capital Cost의 기울기가 Operation Cost의 접선 기울기보다 항상 크다. 따라서 (9, 14, 14, 9)일 때가 가장 Total Cost가 낮고, 에너지도 효율적인 상태임을 알 수 있다. 또한 보편적으로 증류 공정에서는 99%의 순도를 목표로 하므로 현실에서의 쓰임에도 훨씬 가까워졌다고 볼 수 있다.
| Product Spec [2] | [5, 10, 10, 5] | [9, 14, 14, 9] | Cost Change |
| Operation Cost [$/year] | 93,329 | 14,846 | - 78,483 (–84.10%) |
| Capital Cost [$/year] | 22,000 | 39,600 | +17,600 (+80.00%) |
| Total Cost [$/year] | 115,329 | 54,446 | -60,883 (53.79%) |
- ◇이를 통해, 보편적인 순도인 99%를 달성하려는 목표를 세울 때 단 수를 늘리는 것이 Capital Cost를 발생시킨다고 해도 53%라는 커다란 이익을 가져온다는 것을 알 수 있다.
개발 과제 평가
| 평가 항목 | 평가 방법 | 적용 기준 | 개발 목표치 | 비중 (%) | 평가 결과 |
|---|---|---|---|---|---|
| 1. 기본 DWC 모델 | simulation | MESH 방정식을 적용한 기본적인 DWC 모델의 구현 | 단수 추가로 simulation의 확장 가능성 | 20% | 단수를 5,10,10,5로 추가한 모델 구현 |
| 2. 현실적 형태로 정교하게 수정 | 상수 취급한 Cp를 온도의 함수로 수정한 simulation | 참고문헌을 통해 Cp(T)를 다항식화 Cp(T)dT의 적분으로 온도변화 영향 고려 | 온도영향을 고려한 형태로 수정 | 20% | 온도영향을 고려한 형태로 수정 |
| 3. Out Stream에서 각 구성요소 최대화 | RR, BR, F_S를 변수화한 형태로 simulation 발전 | parameter 변수화 out stream의 구성요소 maximize화 | RR, BR, F_S 변수화 이후 objective 설정을 통해 각 구성요소 최대화 확인 | 20% | RR, BR, F_S 변수화 이후 objective 설정을 통해 각 구성요소 최대화 확인 |
| 4. Cost를 고려한 최적의 설계 | Capital, Operation cost를 고려하여 최적의 단수 파악 | 몰분율 및 Cost의 비교로 효율 극대화 alpha, beta 변수화 및 Cost를 고려한 모델 구현 | 비용, 에너지 효율성에 대한 최적화 | 40% | 비용, 에너지 효율성에 대한 최적화 |
개발 과제 관련 향후 전망
◇ Dividing Wall Column(DWC)은 에너지 절감, 공간 절약, 운영비용 절감, 공정 최적화 등 다양한 이점을 제공하는 기술로, 향후 전망이 매우 밝다. 이 기술은 다양한 산업 분야에서 점점 더 많이 채택될 것으로 예상된다. 특히, 에너지 효율성과 환경 규제 준수가 중요한 시대적 흐름 속에서 DWC는 더욱 주목받을 것이다.
◇ 현재 DWC에 대한 실험 연구는 추출, 공비 및 반응 증류 응용의 추가 개발과 구현을 지원하는 지식을 획득하는 데 초점을 두고 있다. 더 나아가, 한층 더 복잡하고 정교한 모델을 개발하고 검증하기 위해, 필요한 실험적 증거를 제공하는 연구도 지속해서 필요하다. DWC는 이미 증류에서 공정 강화를 위한 성공 사례로 간주될 수 있으며, 지속적인 혁신과 발전이 이루어진다면 다양한 산업 분야에서의 활용과 함께 글로벌 시장에서의 경쟁력을 강화할 수 있을 것이다.
◇ 특히, Pyomo와 같은 Python 기반의 오픈 소스 최적화 모델링 언어를 활용한 연구는 DWC 모델링과 최적화를 크게 향상할 것이다. Pyomo를 통해 복잡한 공정을 수학적으로 모델링하고 최적화함으로써 DWC의 상용화를 앞당길 수 있다. 이 과정에서 MESH 방정식을 기반으로 한 모델링 기법은 DWC의 열역학적 우수성을 수치상으로 입증하고, 최적의 운전 조건을 찾는 데 중요한 역할을 할 것이다.
◇ 향후 DWC 기술의 발전은 기술적 측면에서는 정확한 모델링 및 시뮬레이션, 운영비용 감소 및 효율성 향상의 기대효과를 가져올 것이며, 경제적 및 사회적 파급효과 측면에서는 산업 경제성 강화, 지속 가능한 발전 촉진, 기술 혁신과 경쟁력 강화의 파급효과를 가져올 것이다.