천마신교
프로젝트 개요
기술개발 과제
국문 : 초음파 속도를 활용한 벤토나이트 블록의 품질 평가
영문 : Quality Evaluation of Bentonite Blocks Using Ultrasonic Pulse Velocity
과제 팀명
천마신교
지도교수
박도원 교수님
개발기간
2025년 3월 ~ 2025년 6월 (총 4개월)
구성원 소개
서울시립대학교 토목공학과 20228600** 전*(팀장)
서울시립대학교 토목공학과 20198600** 손*준
서울시립대학교 토목공학과 20208600** 오*준
서울시립대학교 토목공학과 20228600** 손*호
서울시립대학교 토목공학과 20228600** 한*혁
서론
개발 과제의 개요
개발 과제 요약
본 개발 과제는 고준위 방사성 폐기물 처분을 위한 공학적 방벽재인 벤토나이트 블록의 품질을 비파괴적으로 평가하기 위한 방법을 제안하고 실험적으로 검증하는 것을 목표로 한다. 기존에는 실험실 규모에서의 품질 평가만이 가능했으나, 본 과제에서는 현장 환경을 고려한 공학 규모의 블록을 직접 성형하고 초음파 검사를 통해 그 품질을 평가하였다. 벤토나이트, 벤토나이트-모래, 벤토나이트-흑연 등 세 가지 시료를 각각 30개씩 총 90개를 제작하고, 다양한 비파괴 검사 기법을 비교한 결과, 초음파 검사가 가장 적합한 방법으로 선정되었다.
초음파 속도와 블록의 건조밀도 및 함수비 간의 관계를 분석하기 위해 회귀 모델과 도달 시간 측정 알고리즘을 개발하였고, 그 결과 초음파 속도는 건조밀도에 선형적으로 비례하며 함수비와도 유의미한 상관성을 보였다. 특히 흑연이 혼합된 BG 시료는 가장 높은 상관계수를 기록했으며, 이는 초음파 속도가 블록의 물리적 특성과 정량적으로 연결될 수 있음을 보여준다.
또한, 임계값 기반 도달 시간 추정 알고리즘을 도입하여 실험의 반복성과 정량성을 확보하였으며, Matlab을 활용한 분석을 통해 초음파 속도 기반의 품질 산정식을 제안하였다. 최종적으로 이 연구는 현장에서 벤토나이트 블록의 품질을 빠르고 경제적으로, 비파괴 방식으로 평가할 수 있는 방법론을 제시하였다는 데 큰 의의가 있다.
개발 과제의 배경
◇ 고준위방사성폐기물 처분에 필요한 압축 벤토나이트 완충재의 불균질성은 완충재 성능 저하의 주요 원인으로 알려져 있음. 고준위방사성폐기물 처분 방법인 심층 처분 개념은 국내 전력 생산량의 30%를 차지하고 있는 원자력 발전 운전을 지속적으로 할 수 있도록 도와주는 역할인 만큼 더 안전한 심층 처분 기술이 필요.
개발 과제의 목표 및 내용
◇ 지금까지는 실험실 규모에서의 완충재 - 벤토나이트 블록 품질평가 방법만이 연구 및 개발됨. 우리는 완충재로써의 벤토나이트 블록이 공학규모 즉, 온도와 습도, 진동 등을 고려하지 않고 현장 상황에 맞는 블록을 직접 성형함. 또한 여러 비파괴 검사 기법들 가운데 평가 기준을 통해 현장에서 품질평가를 할 수 있는 기법을 선정하고자 함
◇ 이를 통해 최종적으로 우리가 성형한 한국원자력연구원에서 제시된 완충재 블록 중 평가 방법에 가장 적합한 블록과 그 방법을 도출
관련 기술의 현황
관련 기술의 현황 및 분석(State of art)
- 전 세계적인 기술현황
● 핀란드/스웨덴: KBS-3V/KBS-3H 방식 개발, MX-80 Na-벤토나이트 사용, 붕괴열 제어에 특화, (Svensk Kärnbränslehantering AB (SKB), Posiva Oy,KBS-3H System Design Phase 2011−2016: Final Report, 2017)
● 스위스: Opalinus Clay 기반 수평처분방식 채택, 자가밀봉(Self-sealing) 특성 활용, (Nagra, Project Opalinus Clay, 2022)
● 캐나다: CANDU 연료에 적합한 HCB(고밀도 벤토나이트) 버퍼박스 사용, 열전도도 향상 기술 적용, (NWMO, 2020)
● 한국: KRS-V(수직)/KRS+(수평) 처분방식 개발 중. 칼슘 벤토나이트 기반 완충재 활용 시도 중, (KAERI, 2008), (KIM et al., 2020)
◇ 심층처분시스템(Deep Geological Disposal, DGD): 고준위 방사성폐기물을 격리하기 위해 지하 깊은 곳 (300~1000m)에 저장하는 방식
◇ 차폐블록 재료: 주요 차폐재로 벤토나이트(Bentonite), 일라이트(Illite), 몬트모릴로나이트(Montmorillonite) 등이 사용됨.
◇ 벤토나이트의 특성: 높은 팽윤성(swelling capacity)과 낮은 투과성으로 방사성 물질의 이동 차단, 높은 이온 교환 능력으로 방사성 핵종의 흡착 가능, 해외에서는 벤토나이트를 차폐재로 채택하여 심층처분 시스템 설계, 포화 시 열전도도: MX-80 → 1.0~1.25 W/(m·K), 국내 Ca-벤토나이트 → 0.8 W/(m·K)
◇ 프로그램 및 수치해석 방법: MATLAB 기반 데이터 분석 수행, 2D 및 3D 선형회귀분석을 통해 건조밀도와 수분함량에 따른 초음파 속도 변화 정량 분석
- 기술 로드맵
◇ 1단계 (~ 2025년 4월): 벤토나이트 블록의 기초 물성 파악 및 기존 해외 심층처분 시스템 (KBS-3V, KBS-3H 등) 조사
◇ 2단계 (~ 2025년 5월): MATLAB을 활용한 기초 선형 회귀모델 구현 (2D, 3D), 실험 기반 데이터 확보를 통한 열-수리-역학 특성 분석 압축강도, 초음파 속도, 수분 함량과 건조 밀도간의 상관관계 정량화
◇ 3단계 (~ 2025년 6월): 최적의 완충재 조건 도출 및 국내 지질 환경에서 적합한 현장 검증 방안 도출
관련 시장에 대한 분석
- 기존/경쟁 기술/제품 조사 비교
- 시장성 분석
◇ 시장 동향: 전 세계 원전 운영국의 70% 이상이 고준위 폐기물 심층처분 연구를 진행 중인 만큼 고준위 방사성 폐기물의 심층처분 필요성이 전 세계적으로 대두되며, 관련 기술 수요는 지속 증가 중. 2030년까지 OECD 국가 중심으로 심층처분장 상용화 예정
◇ 국내 상황: 2032년 이후 원전 저장시설 포화 예정. 현재 심층처분시설 부재로 기술 확보가 시급. 벤토나이트 완충재는 연 1000톤 이상 필요 추정
◇ 사업화 가능성: 벤토나이트 물성 개선 기술(특히 열전도도 향상) 및 MATLAB 기반 분석 모델은 향후 국내 처분시스템 적용성 높음. 관련 산업(토목/광물/핵연료 기술)과 융합 가능
- 사회성 분석
◇ 환경보호: 고준위 폐기물의 안전한 처분을 통해 지하수 및 토양 오염 위험 저감
◇ 국민 안전성 확보: 심층처분 기술의 안정성은 국민 신뢰와 직접 연계되며, 기술 확보 시 사회적 수용성 상승
◇ 규제 대응성: STUK (핀란드), ENSI (스위스), CNSC(캐나다) 기준 비교 후 국내 표준화 기반 마련
개발과제의 기대효과
기술적 기대효과
◇ 기존 코어를 대상으로 수행된 품질 평가 방식과 비교해 물리탐사 자료를 기반으로 광역 범위에 대해 품질 평가가 가능하므로 블록 성형의 효율성과 공학적 방벽재 품질의 신뢰성을 대폭 향상시킬 수 있을 것으로 기대됨. ◇ 고기능성 공학적 방벽재 제작시 제작된 블록의 사전 품질 평가를 통해 비균질성으로 인한 방벽재 성능의 불확실성을 제거함으로써 처분 안정성을 강화하고 최적의 블록 제작 조건 도출을 위한 참고 자료 제공 가능 ◇ 기존 제한된 코어 정보를 기반으로 내삽과 외삽을 통한 물성치 추정이 아니라 비파괴 물리탐사를 통해 연속적인 비파괴 정수 획득이 가능하므로 보다 정확한 공간분포 평가 가능
경제적, 사회적 기대 및 파급효과
◇ 코어링을 활용한 품질 평가 물량을 최소화하고 공학규모 이상 블록 전체에 대한 평가 정수를 신뢰성 있게 결정함으로써 저비용 고효율 품질 평가 가능
◇ 고준위방사선폐기물 심층처분 방식의 중요성이 대두되고 있는 시점에서 공학절 방벽제의 신뢰성 있는 평가 기술 개발은 관련 핵심 기술을 확보하고 대외 경쟁력 강화에 기여 가능성
◇ 공학적방벽재의 배합, 제작 과정에서 불확실성을 줄이고 발생 가능한 결함을 사전에 파악 및 조치함으로써 대규모 재난, 재해로 인한 사회적 비용을 방지
◇ 최근 지속가능한 에너지원으로 원자력 에너지를 활용하기 위해 처분 안정성에 대한 국민의 신뢰 확보가 필수적인 상황에서 고준위폐기물의 장기안정성에 중요한 역할을 하는 공학적방벽재의 품질 신뢰성을 보장함으로써 원자력 에너지 국민 수용성 증대
설계
설계사양
개념설계안
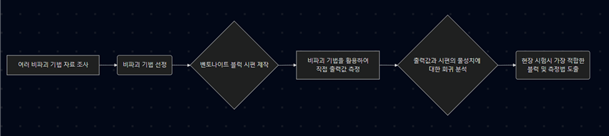
◇ 개념 설계 프로세스
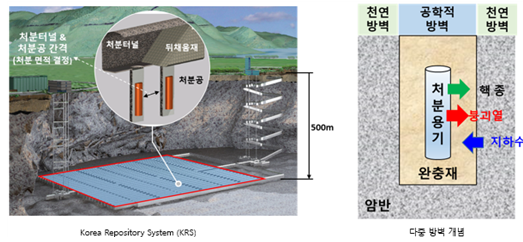
◇ 심층처분 시스템 및 다중 방벽 개념 및 완중재의 거동 - 심층처분 = 지하 500m 암반지대에 고준위폐기물을 직접 처분하는 개념 - 다중방벽 = 공학적 방벽 (처분용기, 완충재, 뒤채움재) + 천연방벽
◇ 공학규모로 한국원자력 연구원에서 제시한 3가지 완충재 – 벤토나이트 블록을 직접 성형. 실험실 규모 즉, 온도, 습도, 압력과 진동 등이 아닌 실제 이용되는 벤토나이트와 모래, 흑연을 통하여 여러 외부 요인을 통제하지 않고 직접 3가지 종류의 시편을 성형.
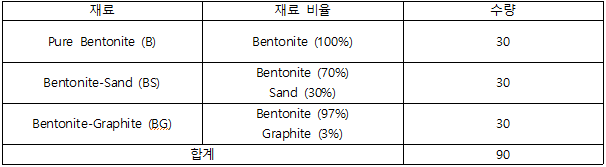
시편의 제원은 용이한 성형을 위하여 직경: 11.4cm, 두께: 3.8cm 로 제작하여 부피 약 387.87cm3로 시편을 제작. 블록은 한국원자력연구원에서 제시한 Pure bentonite, Bentonite-Sand, Bentonite-Graphite를 제작하며, 비율은 각각 10:0, 7:3, 97:3 의 비율로 제작. 시편은 종류별로 30개씩 90개 제작 예정. (이득환 et al. (2022))
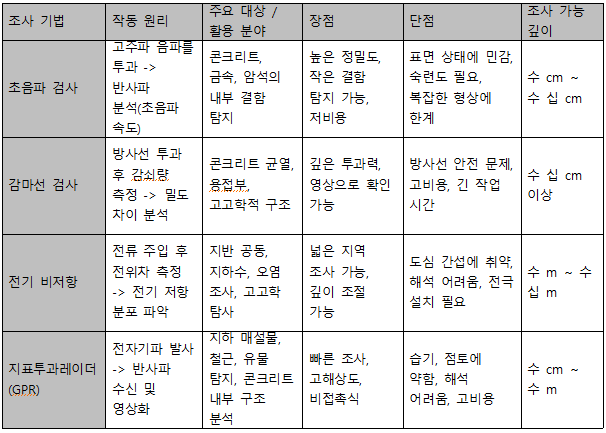
◇ 비파괴 기법 종류
평과 결과를 바탕으로 초음파 시험을 최적의 비파괴 기법으로 선정했다. 초음파 시험은 높은 대역의 주파수를 활용하여 블록 내부의 미세한 불균질성까지 정밀하게 탐지 가능하다. 또한 젤을 바르지 않고 Dry Point 탐촉자를 활용함으로써 실제 적용 환경에서 대규모 블록이나 복잡한 형상에 대해서도 반복적이고 효율적인 시험 수행이 가능하다. 다른 후보 기법으로는 초 분광 근적외선 카메라 기법과 감마선 기법이 고려되었다. 초분광 근적외선 카메라는 비파괴적으로 표면 분석에 강점을 보였으나, 시료 내부까지 촬영이 불가능하다는 한계가 있었다. 감마선 기법은 높은 투과력을 가지고 있지만 최근 핵종 수입 금지와 핵종의 반감기 초과로 인해 측정값의 신뢰도가 떨어지고, 장비 운용의 어려움으로 인해 최종적으로 제외한다.
◇ 완충재 블록의 품질 평가가 가능한 정수 결정
기존 벤토나이트 완충재에 다양한 물질을 첨가하여 성능을 개선한 고기능성 완충재 블록의 품질 평가를 위한 주요 정수를 결정하였다. 심층 처분시설에서 공학적 방벽재는 사용 후 핵연료로부터 발생하는 붕괴열과 지하수의 유입을 최소화하는 핵심 역할을 수행하므로, 열전도도와 수리전도도는 공학적 방벽재의 중요한 품질 평가 지표로 간주한다. 최근 연구에 따르면 아래 그림과 같이 건조밀도와 함수비(포화도)가 열전도도 및 수리전도도와 높은 상관관계 갖는 것이 확인되었다. 이를 바탕으로 초음파 기법을 활용해 건조밀도와 함수비를 측정하고 이를 통해 공학적 방벽재의 품질 평가를 수행할 계획이다.
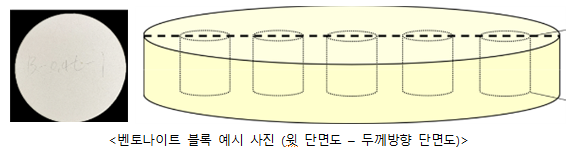
◇ 완충재 블록
초음파 속도를 종속변수로, 선정된 품질 평가 정수인 건조밀도와 함수비를 독립변수로 설정하여, 독립변수의 변화가 종속변수인 비파괴 물성에 미치는 영향을 분석. 이를 위해 품질 평가 정수값이 서로 다른 다수의 코어를 제작하였으며 이러한 품질 변동성을 가진 코어를 대상으로 초음파 속도를 측정하여 분석 할 계획이다.
완충재 블록은 첨가제 비율에 따라 아래 표와 같이 세 가지(B, BS, BG)로 분류 각각 30개 총 90개 블록을 제작한다.
◇ 품질 변동성을 가지는 코어를 대상으로 비파괴 시험 데이터베이스 구축
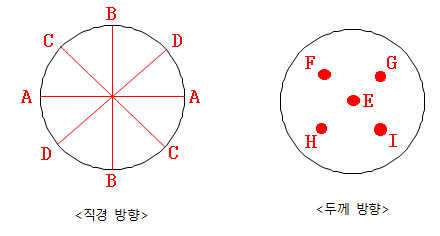
블록의 대표 초음파 속도값을 도출하기 위해, 초음파 속도를 아래 그림과 같이 완충재 코어의 [직경(11.4cm) 및 두께(3.8cm)] 방향에서 측정. 각 지점(A~I)에서 20회를 반복 측정하고 신호 도착 시간을 기준으로 최댓값 2개와 최솟값 2개를 제외하여 대푯값을 산출한다. 또한 지점별 측정값 오차가 ±5% 이내인 경우(e.g. A지점과 E지점의 초음파 도달 시간 간의 오차)에 유의미한 값으로 여기며, 그 초과 오차를 나타내는 값은 버린다.
◇ 비파괴 검사 출력값과 물성치 – 함수비, 건조밀도 간의 상관관계 파악
지금까지 많은 연구에서 각기 다른 물질을 통하여 회귀 분석을 한 것과 같이, 우리는 Matlab을 활용하여 선정된 비파괴 검사를 통해 출력된 값 (e.g. 초음파-초음파속도, GPR-반사파 속도 등)과 시편의 물성치 – 함수비, 건조밀도 간에 회귀분석 (Fitting)을 진행하여 γ(=Gamma, 상관계수) or R2(결정계수)를 구한다. 이를 통하여 비파괴 검사가 얼마나 의미 있는지 파악하고 최종적으로 가장 적합한(결정계수 등이 1에 가까운) 시편과 그 방법을 현장에서 블록에 가장 시험하기에 가장 적합한 결과로 제시하고자 한다.
이론적 계산 및 시뮬레이션
◇ 시간 결정 알고리즘 개발
초음파 신호 도착 시간은 초음파 장비를 통해 얻어낸 그래프를 통해 대체로 육안으로 판별이 가능했으나, 보다 정량적이고 일관된 결과를 얻기 위해 도착 시간 결정 알고리즘을 개발하기로 하였다.
이 때, 초음파 속도 측정 기본원리를 보게 된다면, 초음파 속도 v는 다음과 같은 기본식으로 계산된다.
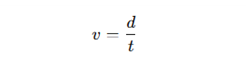
d: 초음파가 이동한 거리 (예: 시험체 두께) t: 초음파의 전파 시간 (송신기에서 수신기까지 도달 시간)
따라서 핵심은 신호의 ‘정확한 도달 시간 t’를 추정하는 것이며, 이를 위해 대표적으로, 임계값 기법과 STA/LTA 기법이 활용된다.
1. 임계값(Threshold) 기반 도달 시간 추정
원리
임계값 기반 방법은 신호의 진폭이 사전에 설정한 특정 임계값을 초과하는 시점을 도달 시간으로 판단하는 방식이다. 보통 가장 먼저 임계값을 초과하는 순간을 초음파 도달 시점으로 간주한다.
장점
구현이 간단하고 계산량이 적다.
단점
노이즈에 민감하며, 임계값 설정이 어렵다. 신호 진폭이 작거나 잡음이 클 경우 잘못된 도달 시간 검출 가능성이 높다.
알고리즘 흐름
1. 초음파 수신 신호를 확보한다.
2. 신호를 절대값 또는 에너지 형태로 변환한다.
3. 임계값을 설정한다 (경험적으로 또는 자동화 방식으로).
4. 신호가 임계값을 최초로 초과하는 시점을 도달 시점으로 정의한다.
2. STA/LTA (Short-Time Average / Long-Time Average) 방법
원리
STA/LTA 방법은 신호의 변화량을 이용하여 도달 시점을 검출하는 방식이다. STA(단기 평균)는 짧은 시간 구간의 측정값을, LTA(장기 평균)는 긴 시간 구간의 측정값을 나타내며, 이 두 값의 비를 계산하여 급격한 변화점을 포착한다.
장점
노이즈에 강하고, 자동화된 시스템에 적합하다. STA/LTA 설정이 적절하면 정확한 도달 시점 추정이 가능하다.
단점
창 길이(STA/LTA) 및 임계값 설정이 결과에 큰 영향을 준다. 설정이 부적절할 경우 오탐지 가능성이 있다.
알고리즘 흐름
1. 수신 신호를 획득한다.
2. 신호의 절대값 또는 제곱 값을 기반으로 STA, LTA를 계산한다.
STA: 짧은 시간창 (예: 1~5ms) LTA: 긴 시간창 (예: 10~50ms)
3. STA/LTA 비율을 계산한다.
4. 해당 비율이 특정 임계값을 초과하는 첫 시점을 도달 시간으로 판단한다.
상세설계 내용
◇ 시간 결정 알고리즘 개발 임계값 기법과 STA/LTA 기법 두 가지 방법 중 벤토나이트 블록은 실험실에서 측정된 초음파 신호의 SNR(신호 대 잡음비)이 비교적 높고, 신호 형태도 명확하게 구분된다. 따라서 복잡한 STA/LTA 방법보다 임계값 기반의 간단한 피킹 방법으로도 충분히 도달 시간을 정확히 추정할 수 있고 구현이 쉬우며, 반복 실험에서 일관성 있고 빠른 분석이 가능하다는 점 특히나 가장 중요한 점은 임계값을 시료와 사용 주파수에 따라서 원활히 조정(피킹)할 수 있는 임계값 방법(Threshhold)를 사용하여 알고리즘을 개발하기로 하였다.
위의 방법을 통하여 개발한 알고리즘은 아래의 코드와 같으며, Matlab을 이용하였다. 또한 임계값(Threshold)은 임의의 값(아래는 50)으로 설정하였다.
% .csv 파일 목록 가져오기
csvFiles = dir(filePattern);
% 주변 값을 더할 개수 설정
numSurroundingValues = 10; % 사용자가 설정할 수 있는 값
% 결과 저장을 위해 파일 열기
fileID = fopen(outputFileName, 'w');
% 도착 시간을 저장할 배열 초기화
arrivalTimes = cell(1, length(csvFiles));
fileNames = {csvFiles.name};
% 각 파일에 대해 반복
for k = 1:length(csvFiles)
% 현재 파일의 전체 경로
baseFileName = csvFiles(k).name;
fullFileName = fullfile(folderPath, baseFileName);
% CSV 파일 불러오기
data = readmatrix(fullFileName);
% 데이터의 행을 하나의 벡터로 통합
originalData = data(:); % 모든 행을 열 벡터로 변환
combinedData = abs(originalData); % 절대값 적용
% 분석하고자 하는 구간 설정
startIdx = 500;
endIdx = 5000;
if endIdx > length(combinedData)
endIdx = length(combinedData); % 구간 설정이 전체 데이터 길이를 초과하지 않도록 조정
end
selectedData = combinedData(startIdx:endIdx);
% 사용자가 제시한 특정 숫자
thresholdExceeds = 50; % 초과할 때의 임계값
% 주변 값을 더하여 평균 계산
smoothedData = movmean(selectedData, numSurroundingValues);
% threshold를 초과하는 첫 번째 데이터의 전체 파일 내 위치 찾기
exceedsThreshold = find(smoothedData > thresholdExceeds, 1, 'first') + startIdx - 1;
if isempty(exceedsThreshold)
fprintf('지정된 구간 내에서 조건을 만족하는 데이터가 없습니다: %s\n', baseFileName);
fprintf(fileID, 'File: %s, Arrival Time: Not Found\n', baseFileName);
arrivalTimes{k} = NaN; % 도착 시간을 NaN으로 표시
else
arrivalTime = exceedsThreshold / 25; % 도착 시간을 계산
fprintf('도착 시간은 %.2fus입니다\n', arrivalTime);
fprintf(fileID, 'File: %s, Exceeds Threshold at: %d, Arrival Time: %.2fus\n', baseFileName, exceedsThreshold, arrivalTime);
arrivalTimes{k} = arrivalTime;
end
◇ 회귀 분석 알고리즘 개발
회귀 분석 알고리즘은 선형뿐만 아니라 다항함수까지 회귀분석이 가능한 Matlab의 기존 내장 코드인 polyfit 함수를 사용하였다. 해당 알고리즘 코드는 아래와 같으며, 임의의 재료(RC시료)를 직접 측정하여 얻은 값을 사용하여 예시 그래프를 도시했다.
% Function to calculate linear regression coefficients and R2
function [coeffs, R2] = linear_regression(X, Y)
coeffs = polyfit(X, Y, 1);
Yfit = polyval(coeffs, X);
SSresid = sum((Y - Yfit).^2);
SStotal = (length(Y) - 1) * var(Y);
R2 = 1 - SSresid/SStotal;
end
% Diameter direction models
disp('Diameter direction models:')
% Model 1: z1 ~ x1
[coeffs1_x, R2_1_x] = linear_regression(x1', z1');
disp(['Model 1 (UPV ~ Dry Density): y = ' num2str(coeffs1_x(1)) '*x + ' num2str(coeffs1_x(2)) ' R^2 = ' num2str(R2_1_x)])
% Model 2: z1 ~ y1
[coeffs1_y, R2_1_y] = linear_regression(y1', z1');
disp(['Model 2 (UPV ~ Water Content): y = ' num2str(coeffs1_y(1)) '*x + ' num2str(coeffs1_y(2)) ' R^2 = ' num2str(R2_1_y)])
% Model 3: z1 ~ x1 + y1
X1 = [x1' y1'];
coeffs1_xy = regress(z1', [ones(size(X1, 1), 1) X1]);
Yfit1 = [ones(size(X1, 1), 1) X1] * coeffs1_xy;
SSresid1 = sum((z1' - Yfit1).^2);
SStotal1 = (length(z1) - 1) * var(z1);
R2_1_xy = 1 - SSresid1/SStotal1;
disp(['Model 3 (UPV ~ Dry Density + Water Content): y = ' num2str(coeffs1_xy(2)) '*x1 + '
num2str(coeffs1_xy(3)) '*y1 + ' num2str(coeffs1_xy(1)) ' R^2 = ' num2str(R2_1_xy)])
% Depth direction models
disp('Depth direction models:')
% Model 1: z2 ~ x2
[coeffs2_x, R2_2_x] = linear_regression(x2', z2');
disp(['Model 1 (UPV ~ Dry Density): y = ' num2str(coeffs2_x(1)) '*x + ' num2str(coeffs2_x(2)) ' R^2 = ' num2str(R2_2_x)])
% Model 2: z2 ~ y2
[coeffs2_y, R2_2_y] = linear_regression(y2', z2');
disp(['Model 2 (UPV ~ Water Content): y = ' num2str(coeffs2_y(1)) '*x + ' num2str(coeffs2_y(2)) ' R^2 = ' num2str(R2_2_y)])
% Model 3: z2 ~ x2 + y2
X2 = [x2' y2'];
coeffs2_xy = regress(z2', [ones(size(X2, 1), 1) X2]);
Yfit2 = [ones(size(X2, 1), 1) X2] * coeffs2_xy;
SSresid2 = sum((z2' - Yfit2).^2);
SStotal2 = (length(z2) - 1) * var(z2);
R2_2_xy = 1 - SSresid2/SStotal2;
disp(['Model 3 (UPV ~ Dry Density + Water Content): y = ' num2str(coeffs2_xy(2)) '*x2 + '
num2str(coeffs2_xy(3)) '*y2 + ' num2str(coeffs2_xy(1)) ' R^2 = ' num2str(R2_2_xy)])
결과 및 평가
완료 작품의 소개
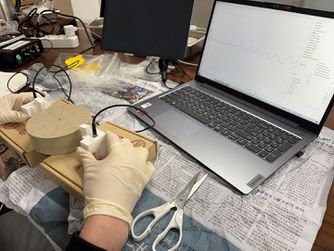
실험 과정 사진
품질 변동성을 가지는 코어를 대상으로 비파괴 시험 데이터베이스 구축
각 블록에 대해 초음파 P파 50kHz와 100kHz로 측정하였다. 초음파 도착 시간은 진폭 값이 임계값(threshold)을 초과하는 첫 번째 지점을 기준으로 결정하였으며, 임계값은 각 시료 및 주파수에 따라 달라진다. 각 지점에서 일관된 도착 시간을 도출하기 위해 예상 도착 시간 범위를 추정하여 해석 구간을 설정한 뒤 해당 구간 내에서 임계값을 적용하여 도착 시간을 최종적으로 산출하였다.
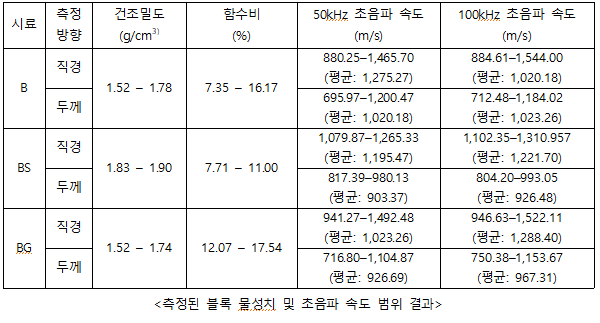
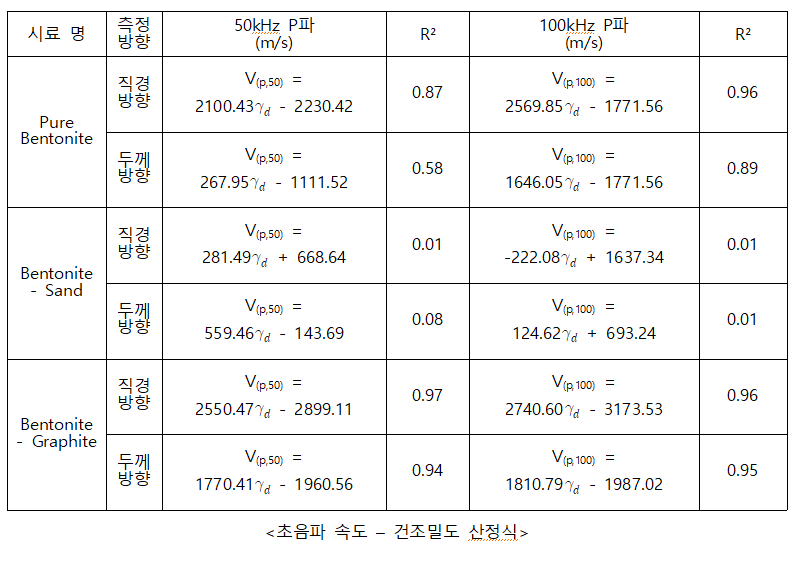
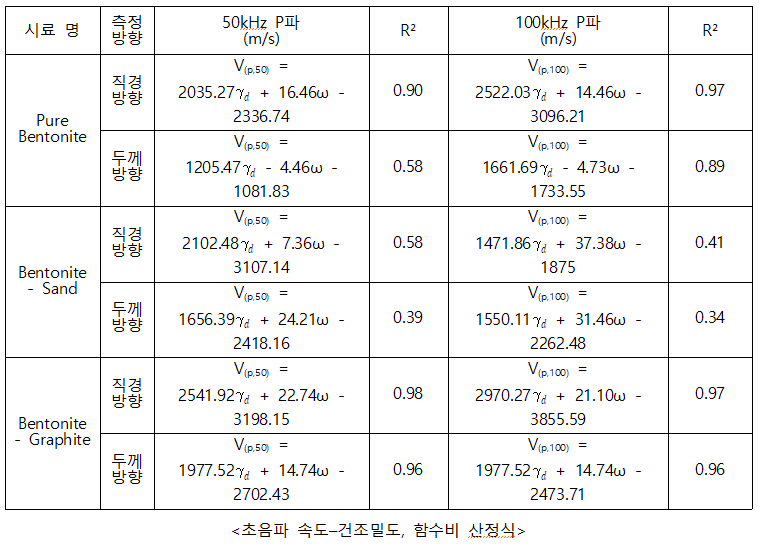
비파괴 물성으로부터 품질 평가 정수 산정식 제안
앞서 수집된 데이터베이스를 바탕으로 비파괴 물성과 품질 평가 정수 간의 상관성을 분석하고, 신뢰도 높은 상관식을 제안했다. 재료(B, BS, BG)에 따른 초음파 속도와 물성치(건조밀도, 함수비)의 상관관계를 종합적으로 분석하였으며, 이를 바탕으로 초음파 속도 기반의 산정식을 도출하였다. 본 과제에서 진행한 회귀분석은 선형회귀분석이기 때문에 결정계수(R²)가 아닌 상관계수()를 고려해야 한다. 하지만 MATLAB의 특성상 결정계수만을 나타내기에 상관관계를 판단하는 데에 있어 결정계수를 이용했으며, ‘R² 값이 0.85 이상인 경우 상관성이 높다.’는 기준을 설정했다.
초음파 속도-건조밀도 산정식 제안
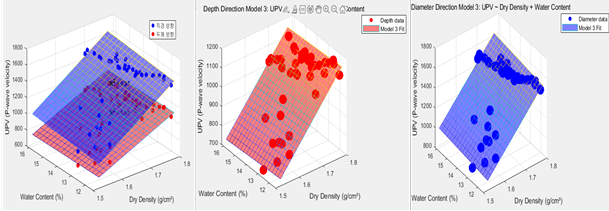
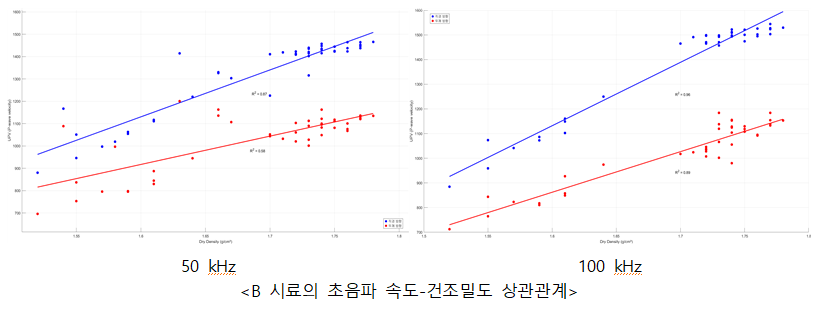
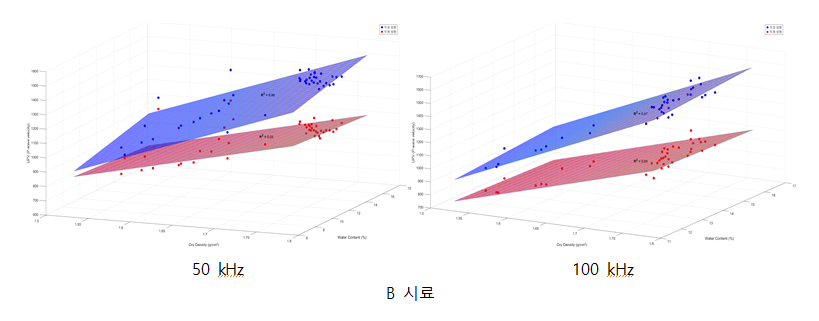
B 시료의 경우, 초음파 속도와 건조밀도 간의 상관관계는 두께 방향을 제외한 모든 조건에서 R² 값이 0.85 이상의 상관성을 보였다. 아래 그림에서 볼 수 있듯이, 직경 방향의 속도가 두께 방향의 속도보다 더 높게 관찰되었으며 이는 모든 시료에서 공통적으로 관찰되었다.
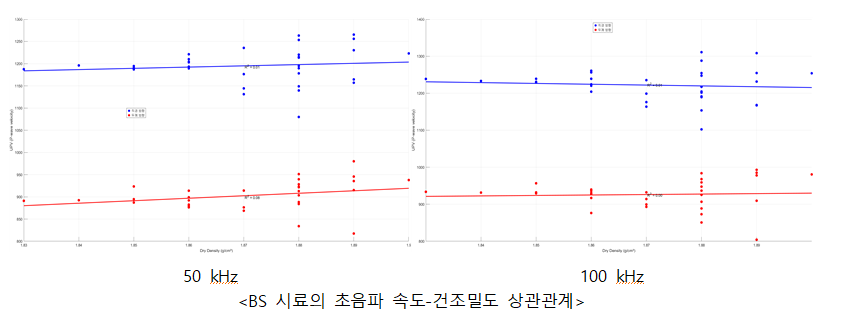
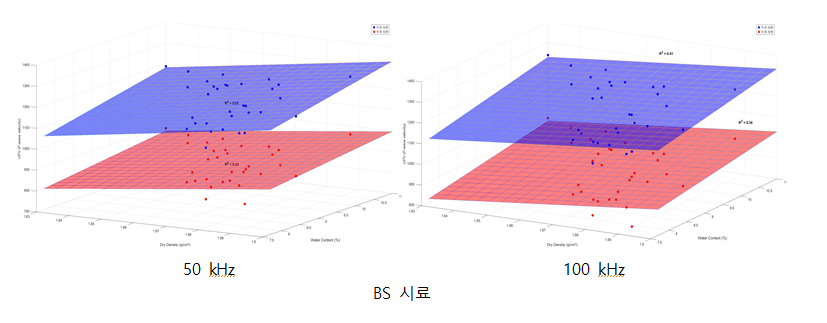
BS 시료의 경우, 건조밀도와 함수비 모두 초음파 속도와 낮은 상관관계를 보였다. 해당 시료들의 경우 건조밀도의 범위가 0.07g/cm3로 좁으며, 모래가 다량(30%) 포함되어 있을 경우 건조밀도의 변화에 대한 초음파 속도의 민감도가 크지 않은 것으로 보인다. 또한, 시료 내 균열에 상대적으로 취약했을 것으로 추정된다. 실제로 BS 시료 중 일부는 초음파 도착 속도를 판별할 수 없거나, 초음파 속도가 측정 불가능할 정도로 손상이 발생하였다. 이러한 문제를 해결하기 위해 초음파 데시벨을 증가시키거나 균열이 발생한 지점을 피해서 측정하는 방법을 적용하여 초음파 속도를 측정하였지만, 이러한 시도에도 불구하고 도착 시간 판별이 어려운 경우가 일부 존재했다.
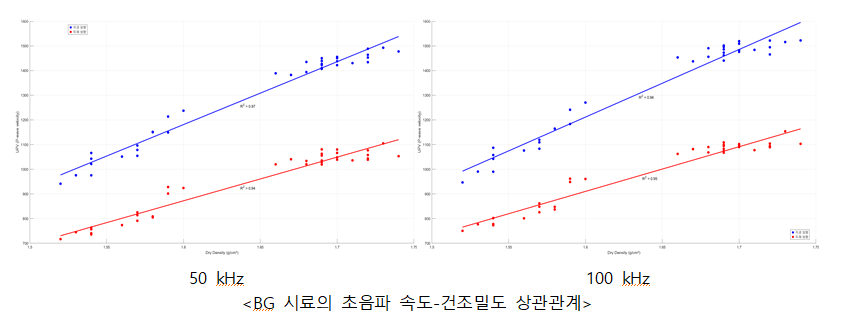
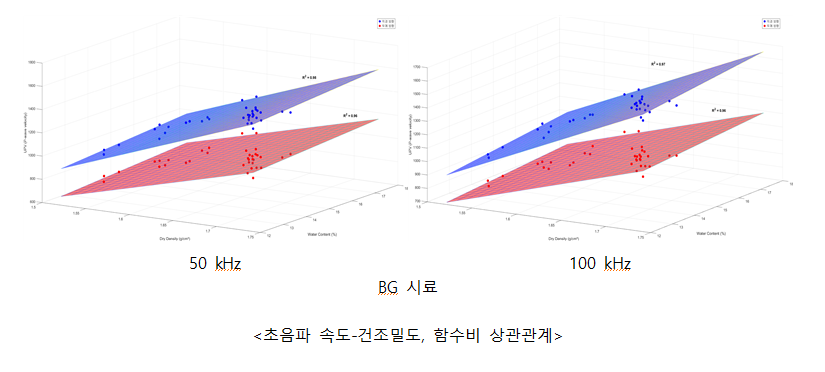
BG 시료의 경우, 측정 방향과 주파수에 상관없이 모든 조건에서 가장 높은 상관성을 보였다.
세 가지 시료의 초음파 속도-건조밀도 상관관계를 종합적으로 분석한 결과 건조밀도가 증가할수록 초음파 속도가 선형적으로 증가하는 경향을 보인다. 이는 밀도가 높을수록 재료가 더 조밀해지고 초음파가 더 빠르게 전달된다는 물리적 특성을 반영한다. B, BS, BG의 세 가지 재료를 대상으로 초음파 속도와 건조밀도 간의 산정식을 도출하였으며, 다음 표에 제시하였다. 분석 결과 손상이 의심되는 BS 시료와 B 시료의 50 kHz 두께 방향 데이터를 제외한 모든 조건에서 R² 값이 0.85 이상으로 높은 상관관계를 보여주었으며, 비파괴 품질 평가 기법의 유효성을 입증했다.
초음파 속도-건조밀도, 함수비 산정식 제안
초음파 속도-건조밀도 산정식의 신뢰도를 향상시키기 위해 기존 초음파 속도-건조밀도 상관 분석에서 함수비를 추가해 분석을 수행했다. 모든 시료에서 정확도의 향상이 확인되었으며, 특히 상관성이 낮았던 BS 시료에서도 정확도가 향상되었다. 초음파 속도는 건조밀도와 함수비에 모두 비례하는 경향성을 보여주었으나, 함수비보다는 건조밀도에 더 민감하게 반응했다.
평가 및 결론
본 과제에서는 고준위 방사성 폐기물 심층 처분을 위한 공학적 방벽재인 벤토나이트 블록의 품질을 비파괴 방식으로 평가하기 위한 방법으로 초음파 속도 기법을 제안하고, 실험을 통해 그 유효성을 검증하였다.
총 90개의 시료(B, BS, BG 각 30개)를 성형하고 초음파 속도를 활용해 초음파속도-건조밀도 및 함수비 상관관계를 분석한 결과, 초음파 속도는 건조밀도에 선형적으로 비례하며, 함수비와도 유의미한 관계를 나타냈다. 특히 BG(Bentonite-Graphite) 시료는 모든 측정 조건에서 가장 높은 상관성을 보였으며, B(Pure Bentonite) 시료 역시 직경 방향과 100kHz P파에 대해서는 우수한 결과를 보였다. 반면, BS(Bentonite-Sand) 시료는 시료 내 불균질성 및 손상 등의 영향으로 상대적으로 낮은 상관성을 나타냈다.
또한, 초음파 도달 시간을 추정하는 임계값 기반 알고리즘을 개발하여, 반복 측정 시에도 정량적이고 일관된 분석이 가능함을 확인하였다.
결론적으로, 결정계수(R²)가 0.85 이상인 경우를 기준으로 신뢰 가능한 상관성을 보이는 공학적 방벽재를 판단할 수 있었으며, 이를 기반으로 한 품질 평가 산정식을 제안하였다. 이는 향후 현장에서도 B(Pure Bentonite), BG(Bentonite-Graphite) 시료에 대해 초음파 속도를 기반으로 한 빠르고 경제적이며, 비파괴적인 품질 평가를 가능하게 할 것으로 기대된다.
포스터
참고문헌
◇ 국내 사용후핵연료 심층처분 방안 개발을 위한 국내외 사례연구, TUNNEL & UNDERGROUND SPACE, 2025
◇ KAERI. (2021). 처분환경에서의 공학적방벽재의 특성 및 상호작용 비파괴 평가, 한국해양대학교 위탁 보고서
◇ Benaicha, M, Jalbaud, O, Roguiez X, Alauoi, A. H.& Burtschell, Y. (2015). Prediction of Self-Compacting Concrete homogeneity by ultrasonic velocity. Alexandria Engineering Founal, 54(4), 1181-1191
◇ 이득환. (2023).공학규모 고기능성 공학적 방벽재개발: Task 3.1 공학규모완충재제작 발표자료
◇ 김창렬, 김정호, 박삼규, 박영수, 이명종, 손정술, & 임형래. (2006). 물리탐사 기술의 석회암 지반침하 지역 공동탐지 적용성연구. 지구물리와 물리탐사,9(4), 271-278
◇ Lee,S. K. (2010). Suggestions for the Physical Property Measurements and theirDatabase. 한국지구물리탐사학회: 학술대회논문집,9-14.
◇ 임환희, 전에녹, 이득환, 전준서, & 이승래. (2019). 초분광근적외선 영상 기술을 이용한 흙의 함수비측정 기술. 한국지반공학회논문집,35(11), 51-62.
◇ 이득환, 윤석, 김진섭, 이기준, 김지원, 김민준. (2022). 공학규모 벤토나이트-모래 완충재 블록의 성형특성 및 열전도도 평가. 한국지반공학회논문집, 38(12), 113-123.
◇ Park, S., Yoon, S., Kwon, S., Lee, M. S., & Kim, G. Y. (2021). Temperature effect on the thermal and hydraulic conductivity of Korean bentonite buffer material
◇ Yoon, S., Lee, G. J., Lee, D. H., Kim, M. S., Kim, J. T., & Kim, J. S. (2024). Evaluation of Thermal Properties for the Bentonil-WRK Bentonite